5. 2^nd multiplication method

---

The 2^nd method of multiplication is based on the following equality:

a x b = (a + b – r) x r + (a – r) x (b – r)

or

a x b = (a + b – r) x r + (r – a) x (r – b)

This method makes the multiplication calculation easy, especially when the two values to be multiplied are close to each other.

1^st example

For example: 18 x 13

I have chosen the value 10 for the reference which I have represented by "r". Notice how easy the calculation of this multiplication is!

I add up	18+13=31
I subtract 10	31-10=21
I multiply by 10	21x10=210	I memorise 210
I multiply the differences from 10	8x3=24	I add 24 and 210, I get the result 234

You can check that 18 x 13 = 234.

NB. I subtracted the reference 10 in the second step. But, in this case, you may well start by subtracting reference 10 from one of the two values and then adding the rest to the other value. For example, 18-10=8, then add 8+13=21. This makes the calculation a little easier. However, in the following example where both values are less than the reference, you should first add the two values and then subtract the reference from the result.

2^nd example

For example: 8 x 6

That's 48; it must be memorised. But let's apply the method described above, always using the reference 10.

This is useful for understanding the method and also a help if you have not learned all the multiplication tables well.

I add up	8+6=14
I subtract 10	14-10=4
I multiply by 10	4x10=40	I memorise 40
I multiply the differences from 10	2x4=8	I add 8 to 40, I get the result 48

Let us now open a parenthesis. People use their fingers to find the products of numbers between 6 and 9. This way of counting with the fingers can be explained by the method we are studying in this section.

I describe this way of using fingers by taking the same example: 6x8 :

1^st rule: the fingers of both hands are numbered from the little finger to the thumb with the values 6 to 10.

2^nd rule: to calculate 6x8, I have to put finger number 6 (which is the little finger) of the left hand opposite finger number 8 (which is the middle finger) of the right hand. And I imagine a line drawn just above these two fingers

3^rd rule: I count the fingers at the bottom of this line and this is the tens number. In our case it is 1+3=4.

NB. Note that this is equivalent to 6-5+8-5 which is equal to 6+8-10. So we find the formula shown above.

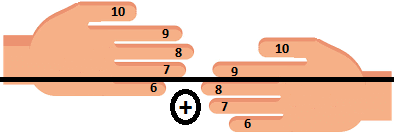
4^th rule: I count the fingers at the top of the line for each hand and multiply them to find the number of units. In our case it is 4x2=8.

NB. Note that this is equivalent to (10-6)x(10-8). So we still find the formula used for our method.

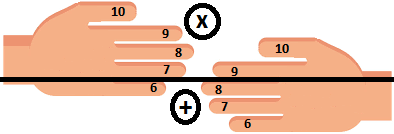
3^rd example

For example: 16 x 7

Here again we will use the reference 10. But notice that one value is greater than 10 while the other is less than 10. When this is the case, the product of the differences from reference 10 should be subtracted, not added.

I add up	16+7=23
I subtract 10	23-10=13
I multiply by 10	13x10=130	I memorise 130
I multiply the differences from 10	6x3=18	I subtract 18 from 130, I get the result 112

Example with 100 as reference

For example: 94 x 109

Both values of the operation are close to 100; let's use 100 as reference:

I add up	94+109     =94+6+109-6     =100+103     =203
I subtract 100	203-100     =103
I multiply by 100	103x100     =10300	I memorise 10300
I multiply the differences from 100	6x9=54	I subtract 54 from 10300, I get the result 10246

Example with 20 as reference

For example: 23 x 29

Let's use 20 as a reference:

I add up	23+29=52
I subtract 20	52-20=32
I multiply by 20	32x20     =32x2x10     =640	I memorise 640
I multiply the differences from 20	3x9=27	I add 27 to 640, I get the result 667

Another example : 31 x 56

1^st solution

Let's use 40 as reference:

I add up	31+56=87
I subtract 40	87-40=47
I multiply by 40	47x40     =47x2x2x10     =94x2x10     =1880	I memorise 1880
I multiply the differences from 40	9x16    =(9x10)+(9x6)    =90+54    =144	I subtract 144 from 1880, I get the result 1736

2^nd solution

31 x 56 = 31 x 28 x 2

We can facilitate this by first calculating 31 x 28 and then multiplying the result by 2.

To calculate 31 x 28, let's use 30 as reference:

I add up	31+28=59
I subtract 30	59-30=29
I multiply by 30	29x30     =(30x30)-30     =900-30     =870	I memorise 870
I multiply the differences from 30	1x2=2	I subtract 2 from 870, I get the result 868

I then multiply 868 by 2, and get the result:

31 x 56 = 1736

Example with double use of the method

For example: 144 x 123

Let's use 100 as a reference:

I add up	144+123=267
I subtract 100	267-100=167
I multiply by 100	167x100     =16700	I memorise 16700
I multiply the differences from 100	44x23     =22x23x2	???

I will reapply the method using reference 20 to calculate 22 x 23. I then multiply the result by 2.

I add up	22+23=45
I subtract 20	45-20=25
I multiply by 20	25x20     =25x2x10     =500	I memorise 500
I multiply the differences from 20	2x3=6	I add 6 to 500, I get the result 506

44 x 23 = 22 x 23 x 2 = 506 x 2 = 1012

An aside: the calculation of 44 x 23 can be done in another way if I notice that 44=11x4 :

23 x 44 = 23 x 11 x 2 x 2 = 253 x 2 x 2 = 506 x 2 = 1012

Let's go back to our main problem. I have stored 16700, I need to add 1012 to it. The result is :

144 x 123 = 17712

Particular cases

Product of 2 values with the same number of tens and whose unit digits complement each other to 10

To calculate the product of 2 values with the same number of tens and whose unit digits complement each other to 10 :

1. Multiply the tens digit by the next digit and put the result in hundreds
2. Calculate the product of the units and add it to the previous result

Example 67 x 63 :

1. Calculate 6 x 7 = 42, I memorise 4 200
2. Calculate 7 x 3 = 21. I add 21 to 4200. The result is 4 221

NB. This is a special case of using the method studied in this section.

Square of a number whose unit digit is 5

To calculate the square of a number whose units digit is 5 :

1. Multiply the tens digit by the next digit and put the result in hundreds
2. Add 25 to the previous result

Example : 35²

1. Calculate 3 x 4 = 12, 
2. The result is 1225.

When the two values are not close to each other

It is possible to use the method when the two values to be multiplied are not close to each other, but using two references:

If one reference is a multiple of the other, use the formula :

a x b = (k x a + b - k x r) x r + (a – r) x (b – k x r)

If both references are multiples of the same value, use the formula :

a x b = (l x a + b x k – k x l x r) x r + (a – k x r) * (b – l x r)

Example : 43 x 18

I use 40 and 20 as references. 40 is a multiple of 20. I therefore use the 1^st formula with k=2 (because 40=20x2)

I add 43 and 18x2 (*)	43+(18x2)       =43+36       = 79
I subtract 40 (**)	79-40=39
I multiply by 20 (***)	39x20    =(40x20)-20    = 800-20    =780	I memorise 780
I multiply the differences from the references	3x2=6	I subtract 6 from 780, I get the result 774 (****)

(*) I multiplied the small value with the factor k
(**) I have subtracted the upper reference
(***) I multiplied by the lower reference
(****) I have subtracted because 43 is higher than its reference 40 and 18 is lower than its reference 20.

Example : 52 x 34

I use 50 and 30 as references. 50 and 30 are multiples of 10 with k=5 and l=3 as factors

I add 52x3 and 34x5 (*)	(52x3)+(34x5)      =156+170      = 326
I subtract 10x3x5 (**)	326-150=176
I multiply by 10 (***)	176x10=1760	I memorise 1760
I multiply the differences from the references	2x4=8	I add 8 to 1760, I get the result 1768

(*) I have multiplied the values with the factors in a crosswise manner
(**) I have subtracted the common divisor of the two references multiplied by the two factors
(***) I have multiplied by 10 which is the common divisor of the two references.

---