البكالوريا الحساب التكاملي

تعريف

لنفترض أن f دالة متصلة على المجال [a ; b] و F دالة أصلية ل f.

تكامل f من a إلى b و الذي نرمز إليه ب ∫ a b f(x) dx يساوي F(b) - F(a).

نكتب :

∫ a b f(x) dx = [ F(x) ] a b = F(b) - F(a)

مثال

حساب التكامل :

خاصية

لتكن f دالة متصلة على المجال [a ; b].

إذا كانت f(x) > 0 على [a ; b] فإن ∫ a b f(x) dx > 0.

إذا كانت f(x) < 0 على [a ; b] فإن ∫ a b f(x) dx < 0.

التكامل بالتجزئة

لنفترض أن u وv دالتان متصلتان على المجال [a ; b] بحيث تكون دالتاهما المشتقتان u ' و v ' متصلتين على [a ; b]. فإن

∫ a b (u(x).v '(x)) dx = [ u(x).v(x) ] a b - ∫ a b (u '(x).v(x)) dx.

المثال 1

حساب التكامل :

I = ∫ 1 2 x e^x dx

نضع :

u(x) = x ⇒ u '(x) = 1

v '(x) = e^x ⇒ v(x) = e^x

إذن

المثال 2

حساب التكامل :

I = ∫ 1 2 x² ln(x) dx

نضع :

u(x) = ln(x) ⇒ u '(x) = 1 / x

v '(x) = x² ⇒ v(x) = 1 / 3 x³

إذن

المثال 3

حساب التكامل :

I = ∫ 0 2 x / √x + 1 dx

نضع :

u(x) = x ⇒ u '(x) = 1

v '(x) = 1 / √x + 1 ⇒ v(x) = 2 √x + 1

إذن

حساب المساحة باستخدام التكامل

لنفترض أن f دالة متصلة على المجال [a ; b].

المساحة المحدَّدة بالمنحنى الذي يمثِّل f، والمستقيمين ذي المعادلتين x=a و x=b ومحور الأفاصيل يساوي ∫ a b |f(x)| dx.

إذن

إذا كانت f(x) > 0 على [a ; b] فإن هذه المساحة تساوي ∫ a b f(x) dx.

إذا كانت f(x) < 0 على [a ; b] فإن هذه المساحة تساوي - ∫ a b f(x) dx.

مثال

نأخذ الدالة f المُعرَّفة ب :

f(x) = x² - x - 2

لنحسب المساحة المحدَّدة بالمنحنى الذي يمثِّل f، والمستقيمين ذي المعادلتين x=1 و x=2 ومحور الأفاصيل.

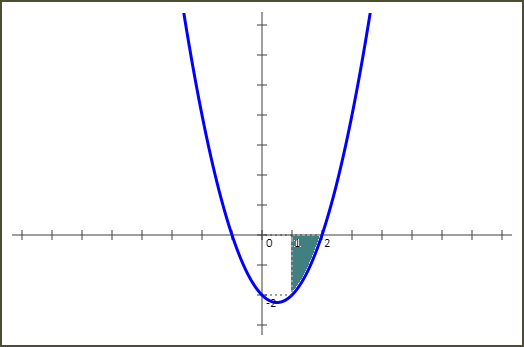
$Calcul de l'aire par l'intégrale$

f(x) سالبة على المجال [1 ; 2]. إذن المساحة المطلوبة تساوي :

لنحسب المساحة المحدَّدة بالمنحنى الذي يمثِّل f، والمستقيمين ذي المعادلتين x=1 و x=3 ومحور الأفاصيل.

$Calcul de l'aire par l'intégrale$

f(x) سالبة على المجال [1 ; 2] وموجبة على المجال [2 ; 3]. إذن المساحة المطلوبة تساوي :

المساحة المحددة بمنحنى دالة و مستقيم

لنفترض أن f دالة متصلة على المجال [a ; b] و D مستقيم معادلته y = ax + b.

المساحة المحدَّدة بالمنحنى الذي يمثِّل f، والمستقيمين ذي المعادلتين x=a و x=b و المستقيم D تساوي ∫ a b |f(x) - y| dx.

إذن

إذا كان Cf فوق D على المجال [a ; b] (أي f(x) > y) فإن هذه المساحة تساوي ∫ a b (f(x) - y) dx.

إذا كان Cf تحت D على المجال [a ; b] (أي f(x) < y) فإن هذه المساحة تساوي - ∫ a b (f(x) - y) dx.

مثال

نأخذ الدالة f المُعرَّفة ب :

f(x) = x² - x - 2

نعتبر مستقيم D معادلته :

y = 2x - 8

لنحسب المساحة المحدَّدة بالمنحنى الذي يمثِّل f، والمستقيمين ذي المعادلتين x=-3 و x=-2 والمستقيم D.

$Calcul de l'aire par l'intégrale$

Cf فوق D على المجال [1 ; 2]. إذن المساحة المطلوبة تساوي :

لنحسب المساحة المحدَّدة بالمنحنى الذي يمثِّل f، والمستقيمين ذي المعادلتين x=-3 و x=0 والمستقيم D.

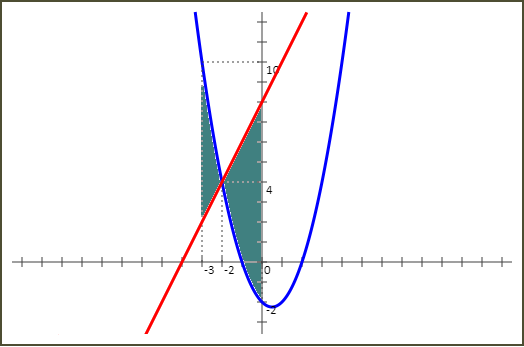
$Calcul de l'aire par l'intégrale$

Cf فوق D على المجال [-3 ; -2] وتحت D على المجال [-2 ; 0]. إذن المساحة المطلوبة تساوي :

المساحة المحصورة بين منحنيَي دالتين

لنفترض أن f و g دالتين متصلتين على المجال [a ; b].

المساحة المحدَّدة بالمنحنى الذي يمثِّل f، والمستقيمين ذي المعادلتين x=a و x=b والمنحنى الذي يمثِّل g تساوي ∫ a b |f(x) - g(x)| dx.

إذن

إذا كان Cf فوق Cg على المجال [a ; b] (أي f(x) > g(x)) فإن هذه المساحة تساوي ∫ a b (f(x) - g(x)) dx.

إذا كان Cf تحت Cg على المجال [a ; b] (أي f(x) < g(x)) فإن هذه المساحة تساوي ∫ a b (g(x) - f(x)) dx.

القيمة المتوسطة لدالة

لنفترض أن f دالة متصلة على المجال [a ; b].

القيمة المتوسطة للدالة f على [a ; b] تساوي 1 / b - a ∫ a b f(x) dx.

تمارين مصححة - حساب التكامل