lim x→-∞ f(x) = lim x→-∞ ( -1 / x + 2 - 2x + 3) = +∞
lim x→-2 x < -2 f(x) = lim x→-2 x < -2 ( -1 / x + 2 - 2x + 3) = +∞
lim x→-2 x > -2 f(x) = lim x→-2 x > -2 ( -1 / x + 2 - 2x + 3) = -∞
lim x→+∞ f(x) = lim x→+∞ ( -1 / x + 2 - 2x + 3) = -∞

2 - حساب الدالة المشتقة وتحديد إشارتها

نواصل مع مثال الدالة العددية f المعرفة كما يلي :

f(x) = -1 / x + 2 - 2x + 3

نحسب الدالة المشتقة :

لإيجاد النقط حيث تنعدم كثيرة الحدود "2x² + 8x + 7"، نحسب المميز

Δ = 8.

نحسب نقط انعدام كثيرة الحدود "2x² + 8x + 7"

x₁ = -4 - √2 / 2
x₂ = -4 + √2 / 2

إذن

f '(x) > 0 في ] -4 - √2 / 2 ; -4 + √2 / 2 [
f '(x) < 0 في ]-∞; -4 - √2 / 2 [ ∪ ] -4 + √2 / 2 ;+∞[

إذن

f تصاعدية في ] -4 - √2 / 2 ; -4 + √2 / 2 [
f تنازلية في ]-∞; -4 - √2 / 2 [ ∪ ] -4 + √2 / 2 ;+∞[

مثال آخر:

لنأخذ الدالة العددية g المعرفة كما يلي :

g(x) = x³ / 8 - 3x / 2 + 1

نحسب الدالة المشتقة :

g '(x) = 3x² / 8 - 3 / 2 = 3 / 8 (x² - 4)

إذن تنعدم الدالة المشتقة في :

x₁ = -2
x₂ = 2

إذن

f '(x) < 0 في ]-2;2[
f '(x) > 0 في ]-∞;-2[ ∪ ]2;+∞[

إذن

f تنازلية في ]-2;2[
f تصاعدية في ]-∞;-2[ ∪ ]2;+∞[

انظر الرابط دراسة إشارة دالة لتقنيات تحديد إشارة.دالة.

3 - جدول التغيرات

جدول تغيرات الدالة هو جدول يوضح اتجاه تغير الدالة بناءً على إشارة الدالة المشتقة.

يبين جدول تغيرات الدالة حدود مجال التعريف بالإضافة إلى النقاط حيث تنعدم الدالة المشتقة. ولذلك فمن الضروري حساب النهايات أو صور هذه النقاط.

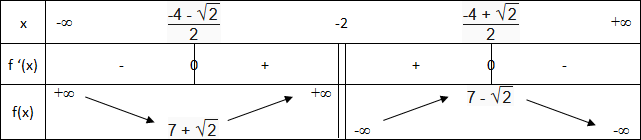
نواصل مع مثال الدالة العددية f المعرفة كما يلي :

f(x) = -1 / x + 2 - 2x + 3

جدول تغيرات الدالة هو :

$دراسة الدوال$

4 - دراسة الفروع اللانهائية

يوضح الجدول التالي الحالات التي يكون فيها التمثيل المبياني لدالة (C) للدالة العددية f له خط مقارب أو فرع شلجمي.

يكون مستقيما هو خط مقارب للمبيان (C)، إذا كان يميل إلى الاقتراب من هذا المستقيم أكثر فأكثر دون أن يتقاطع معه أبداً (انظر الأمثلة في الجدول التالي).

يكون للمبيان (C) فرع شلجمي في اتجاه خط مستقيم بجوار اللانهاية، إذا ظهر عمليًا موازيًا لهذا الخط المستقيم. و لكن في الواقع، يبتعد المنحنى إنما ببطء عن هذا الخط.

المبيان	مثال	النتيجة	النهايات الواجب التحقق منها
$دراسة الدوال$	f(x) = 1 / x - 1 + 1 lim x→1 x < 1 f(x) = -∞ lim x→1 x > 1 f(x) = +∞	يقبل المبيان (C) مقاربا عموديا معادلته x = a	lim x→a f(x) = ±∞
$دراسة الدوال$	f(x) = 1 / x - 1 + 1 lim x→-∞ f(x) = 1 lim x→+∞ f(x) = 1	يقبل المبيان (C) مقاربا أفقيا بجوار ∞ معادلته y = a	lim x→±∞ f(x) = a
$دراسة الدوال$	f(x) = √x lim x→+∞ f(x) / x = 0	يقبل المبيان (C) فرعا شلجميا بجوار ∞ اتجاهه محور الأفاصيل	lim x→±∞ f(x) / x = 0		lim x→±∞ f(x) = ±∞
$دراسة الدوال$	f(x) = -1 / x + 2 - 2x + 3 lim x→±∞ f(x) / x = -2 lim x→±∞ f(x) + 2x = 3	يقبل المبيان (C) مقاربا مائلا بجوار ∞ معادلته y = ax + b	lim x→±∞ (f(x) - ax) = b	lim x→±∞ f(x) / x = a (≠0)
$دراسة الدوال$	f(x) = 2x - √x lim x→+∞ f(x) / x = 2 lim x→+∞ f(x) - 2x = -∞	يقبل المبيان (C) فرعا شلجميا بجوار ∞ اتجاهه المستقيم الذي معادلته y = ax	lim x→±∞ (f(x) - ax) = ±∞	lim x→±∞ f(x) / x = a (≠0)
$دراسة الدوال$	f(x) = x² lim x→-∞ f(x) / x = -∞ lim x→+∞ f(x) / x = +∞	يقبل المبيان (C) فرعا شلجميا بجوار ∞ اتجاهه محور الأراتيب	lim x→±∞ f(x) / x = ±∞

يتبين من الجدول أنه إذا كانت النهاية عند اللانهاية لـ f(x) تساوي اللانهاية، فيجب علينا حساب نهاية f(x) / x . وإذا كانت نتيجة هذه النهاية هي عدد "a" يختلف عن 0، فيجب علينا حساب نهاية f(x)-ax.

و هو الحال بالنسبة للدالة f المعرفة كما يلي :

f(x) = -1 / x + 2 - 2x + 3

لنحسب النهايات

lim x→-∞ f(x) = +∞
lim x→-∞ f(x) / x = -2
lim x→-∞ (f(x) + 2x) = 3

نستنتج أن المستقيم ذو المعادلة y=-2x+3 هو مقارب مائل لمبيان الدالة f بالقرب من -∞. تأكد بنفس الطريقة أن هذا هو الحال أيضًا بالقرب من +∞.

ملحوظة: فيما يتعلق بالمقارب المائل، قد يكون لديك سؤال مختلف.

إما أظهر أن الخط ذو المعادلة y=-2x+3 هو مقارب مائل لمبيان الدالة f بالقرب من ±∞.

أو، احسب النهاية في ±∞ لـ f(x)-(-2x+3). استنتج...

في كلتا الحالتين، عليك حساب نهاية f(x)-(-2x+3) وإذا حصلت على 0، فيمكنك استنتاج أن المستقيم ذو المعادلة y=-2x+3 هو مقارب مائل لـمبيان الدالة f بالقرب من +∞.

5 - دراسة التقعر و التحدب للتمثيل المبياني للدالة

نقول أن مبيان دالة عددية محدب إذا كان المماس عند أي نقطة على هذا المبيان يقع أسفل المنحنى.

نقول أن مبيان دالة عددية مقعر إذا كان المماس عند أي نقطة على هذا المبيان يقع فوق المنحنى.

نقطة الانعطاف هي نقطة يتغير فيها تحدب المنحنى.

$دراسة الدوال$

لدراسة التحدب، يجب حساب المشتقة الثانية للدالة. وهي الدالة المشتقة للدالة المشتقة للدالة. نرمز لها ب f ".

يجب بعد ذلك دراسة إشارة f "(x).

إذا كانت f "(x) > 0 لكل x من المجال I، يكون منحنى الدالة f محدبًا على I.
إذا كانت f "(x) < 0 لكل x من المجال I، يكون منحنى الدالة f مقعرًا على I.
إذا كانت f "(x₀) = 0 مع تغيير الإشارة فإن منحنى الدالة f له نقطة انعطاف عند x₀.

مثال

لنأخذ الدالة g المعرفة بما يلي :

g(x) = x³ / 8 - 3x / 2 + 1

لنحسب الدالة المشتقة :

g '(x) = 3x² / 8 - 3 / 2

لنحسب الدالة المشتقة الثانية :

g "(x) = 3x / 4

إذن :

g "(x) > 0 لكل x > 0 وبالتالي فإن منحنى الدالة g محدب ]0;+∞[.
g "(x) < 0 لكل x < 0 وبالتالي فإن منحنى الدالة g مقعر ]-∞;0[.
g "(0) = 0 مع تغيير الإشارة، وبالتالي فإن لمنحنى الدالة g نقطة انعطاف عند 0.

$دراسة الدوال$

6 - دراسة الوضع النسبي للتمثيل المبياني للدالة

يتم تحديد الوضع النسبي لمبيان الدالة f بالنسبة إلى مستقيم معادلته y=ax+b عن طريق الحساب :

f(x) - y

يجب بعد ذلك تحديد إشارة هذه الصيغة.

إذا كانت f(x) - y > 0 لكل x من المجال I، يكون منحنى الدالة f أعلى المستقيم على I.
إذا كانت f(x) - y < 0 لكل x من المجال I، يكون منحنى الدالة f أسفل المستقيم على I..

قد نستخدم هذه التقنية لتحديد الوضع النسبي لمنحنى بالنسبة إلى الخط المقارب أو بالنسبة إلى المماس.

يمكننا أيضًا دراسة الوضع النسبي لمنحنى دالة f بالنسبة لمنحنى دالة أخرى g :

إذا كانت f(x) - g(x) > 0 لكل x من المجال I، يكون منحنى الدالة f أعلى من منحنى g على I.
إذا كانت f(x) - g(x) < 0 لكل x من المجال I، يكون منحنى الدالة f أسفل من منحنى g على I.

7 - مركز التماثل أو محور التماثل للتمثيل المبياني للدالة

مبرهنة

المستقيم ذو المعادلة y=a هو محور تماثل لمبيان الدالة f، إذا كان لكل عدد x من Df، فإن (2a - x) تنتمي أيضًا إلى Df و

f(2a - x) = f(x)

مبرهنة

النقطة M(a,b) هي مركز تماثل لمبيان الدالة f، إذا كان لكل عدد x من Df، فإن (2a - x) تنتمي أيضًا إلى Df و

f(2a - x) = 2b - f(x)

مثال محور التماثل:

لنأخذ الدالة f المعرفة بما يلي :

f(x) = x² - 2x - 1

لنتحقق من أن المستقيم ذو المعادلة y=1 هو محور تماثل لمبيان الدالة f :

كإشارة، ها هو مبيان الدالة

$دراسة الدوال$

مثال مركز التماثل:

لنأخذ الدالة g المعرفة بما يلي :

g(x) = x³ - 3x² + 3x

لنتحقق من أن النقطة M(1,1) هي مركز تماثل لمبيان الدالة g :

كإشارة، ها هو مبيان الدالة

$دراسة الدوال$

8 - إنشاء التمثيل المبياني للدالة

لإنشاء التمثيل المبياني لدالة يجب :

استخدم جدول التغيرات لرسم المماسات الأفقية، أي عند النقاط حيث تنعدم الدالة المشتقة.
استخدم دراسة التقعر لتحديد نقاط الانعطاف. ارسم مماسات المبيان عند هذه النقاط.
ارسم أيضًا الفروع اللانهائية.

سيتم استخدام هذه العناصر كمعالم لرسم المبيان.

حالة الدالة :

f(x) = -1 / x + 2 - 2x + 3

$دراسة الدوال$