Baccalauréat Etude de signe de fonction
Cas d'une fonction affine
Une fonction affine est une fonction de la forme :
f(x) = ax + b
Une fonction affine s'annule au point -b a . Son tableau de signe est comme suit :
| Signe de a | Tableau de signes |
|---|---|
| a>0 |  |
| a<0 | 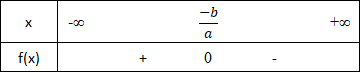 |
Cas d'une fonction polynomiale de degré 2
Une fonction polynomiale de degré 2 est de la forme :
f(x) = ax2 + bx + c
Pour étudier le signe de cette fonction, il faut d'abord trouver les points où elle s'annule. Pour cela, il faut ou bien factoriser son expression ou bien utiliser le discriminant Δ.
Le signe de la fonction est déterminé selon le tableau suivant :
| Signe de Δ | Solutions f(x)=0 | Signe de a | Tableau de signes |
|---|---|---|---|
| Δ>0 | 2 réels x1 et x2 | a>0 |  |
| a<0 | 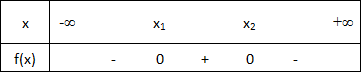 |
||
| Δ=0 | un réel x0 | a>0 |  |
| a<0 |  |
||
| Δ<0 | Aucune solution | a>0 |  |
| a<0 |  |
Cas d'une fonction polynomiale factorisée ou une fonction fractionnaire
Exemple:
Soit la fonction f définie par :
f(x) = (x - 3)(-2x2 + 3x - 1)
Pour trouver les zéros pour le polynôme "-2x2 + 3x - 1", on calcule le discriminant
Δ = 1.
On calcule les zéros pour le polynôme "-2x2 + 3x - 1"
x1 =
1
2
x2 = 1
Le signe de f(x) est comme suit :
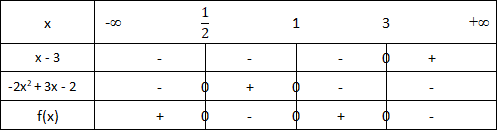
Autre exemple:
Soit la fonction g définie par :
g(x) = 2x2 - 3x - 2 x - 1
Pour trouver les zéros pour le polynôme "2x2 - 3x - 2", on calcule le discriminant
Δ = 25.
On calcule les zéros pour le polynôme "2x2 - 3x - 2"
x1 =
-1
2
x2 = 2
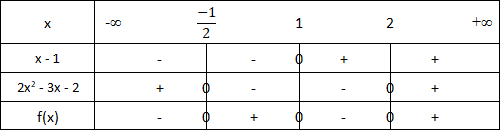
Le signe de g(x) est comme suit :
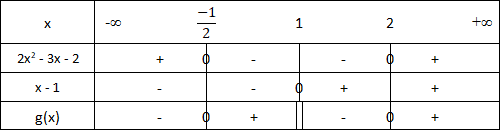
Cas d'une fonction polynomiale de degré 3
Une fonction polynomiale de degré 3 est de la forme :
f(x) = ax3 + bx2 + cx + d
Pour étudier le signe de cette fonction, il faut trouver les points où elle s'annule. Pour cela :
- ou bien factoriser son expression en utilisant une identité remarquable par exemple.
- ou bien on vous demande de vérifier que l'expression s'annule en un point x0. Dans ce cas, cette expression est divisible par "x-x0". Effectuer donc une division euclidienne.
Exemple:
Soit la fonction f définie par :
f(x) = 2x3 - 5x2 + x + 2
Ce polynôme s'annule en 1. Donc, il est divisible par x-1. Effectuons la division euclidienne.
| 2x3 | - 5x2 | + x | + 2 | x | - 1 | |
| -2x3 | + 2x2 | 2x2 | - 3x | - 2 | ||
| -3x2 | + x | + 2 | ||||
| +3x2 | - 3x | |||||
| -2x | + 2 | |||||
| +2x | - 2 | |||||
| 0 |
Donc
f(x) = 2x3 - 5x2 + x + 2 = (x - 1)(2x2 - 3x - 2)
Pour trouver les zéros pour le polynôme "2x2 - 3x - 2", on calcule le discriminant
Δ = 25.
On calcule les zéros pour le polynôme "2x2 - 3x - 2"
x1 =
-1
2
x2 = 2
Le signe de f(x) est comme suit :