Baccalauréat Exercices Etude de signe de fonction
Consulter le cours Etude de signe de fonction
Exercice 1
Soit la fonction numérique f définie par :
f(x) = 6x3 - 11x2 - 4x + 4
- Vérifier que f(x) s'annule en 2.
- Factoriser f(x).
- Déterminer le signe de f(x) et dresser son tableau de signe
Solution
f(2) = 6.23 - 11.22 - 4.2 + 4 = 48 - 44 - 8 + 4 = 0
f(x) est donc divisible par "x-2". Effectuons la division euclidienne.
| 6x3 | - 11x2 | - 4x | + 4 | x | - 2 | |
| -6x3 | + 12x2 | 6x2 | + x | - 2 | ||
| x2 | - 4x | + 4 | ||||
| -x2 | + 2x | |||||
| -2x | + 4 | |||||
| +2x | - 4 | |||||
| 0 |
Donc
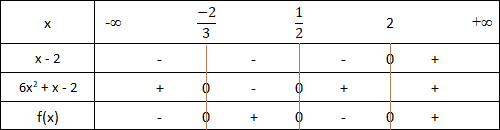
f(x) = 6x3 - 11x2 - 4x + 4 = (x - 2)(6x2 + x - 2)
Pour trouver les zéros pour le polynôme "6x2 + x - 2", on calcule le discriminant
Δ = 49.
On calcule les zéros pour le polynôme "6x2 + x - 2"
x1 =
1
2
x2 =
-2
3
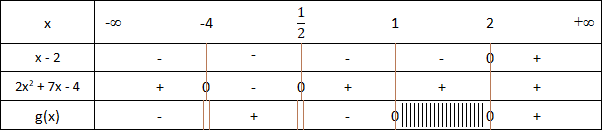
Le signe de f(x) est comme suit :
Exercice 2
Soit la fonction g définie par :
g(x) = (x - 2) √x2 - 3x + 2 2x2 + 7x - 4
Déterminer le signe de g(x) et dresser son tableau de signe
Solution
Il faut d'abord déterminer le signe pour le polynôme "x2 - 3x + 2" pour trouver le domaine de définition de la fonction. On calcule le discriminant pour ce polynôme :
Δ = 1.
On calcule les zéros pour le polynôme "x2 - 3x + 2"
x1 = 1
x2 = 2
Le domaine de définition de la fonction g est Dg = ]-∞;1[∪]2;+∞[
Pour trouver les zéros pour le polynôme "2x2 + 7x - 4", on calcule le discriminant
Δ = 81.
On calcule les zéros pour le polynôme "2x2 + 7x - 4"
x1 = -4
x2 =
1
2
Le signe de g(x) est comme suit :