Il nous arrive tous de commettre des erreurs lors d’opérations de calcul. Il y a pourtant un moyen simple de vérifier une opération de calcul et qui est rarement enseignée aux enfants.
Cette méthode de vérification est basée sur la substitution des valeurs impliquées dans l’opération par d’autres valeurs que nous appellerons les substituts. Nous effectuons ensuite l’opération pour les substituts afin de vérifier sa validité.
Le substitut d’un nombre est déterminé par la somme des chiffres de ce nombre. Pour le nombre, 7492 par exemple, la somme des chiffres est
7+4+9+2=22
Mais, tant que nous avons un nombre à plus d’un chiffre, alors nous calculons la somme de ses chiffres. C’est-à-dire pour 22 c’est
2+2=4.
Le substitut pour le nombre 7 492 est donc 4.
Il y a un moyen de simplification. Nous pouvons ignorer les chiffres 9 lors de la détermination du substitut d’un nombre. Nous pouvons également ignorer deux ou plusieurs chiffres dont la somme est 9 ou un multiple de 9. Et nous aurons le même résultat.
Pour notre valeur 7492, je peux ignorer le 9 et je peux ignorer le 7 avec le 2, j’aurai alors uniquement 4 qui est le substitut.
Soit par exemple l’opération :
7492 x 365 = 2734580
1ère étape de vérification
Déterminer les substituts pour les deux valeurs ainsi que celui du produit trouvé :
Pour la 1ère valeur 7492, j’ignore le 9 et j’ignore le 7 avec le 2, le substitut pour la 1ère valeur est 4.
Pour la 2ème valeur 365, j’ignore le 3 avec le 6, le substitut est donc 5.
Pour le produit trouvé 2734580, j’ignore le 2 avec le 7 et le 4 avec le 5, j’aurai donc 3+8=11 et 1+1=2. Le substitut pour le produit trouvé est 2.
2ème étape de vérification
Dessiner une croix comme à l’image ci-dessous. Ecrire le substitut de la 1ère valeur en haut, celui de la 2ème en bas et celui du résultat trouvé à gauche.
3ème étape de vérification
Multiplier le substitut de la 1ère valeur par celui de la 2ème valeur. C’est 4x5=20. Et tant que nous avons un nombre à plus d’un chiffre, alors nous calculons la somme de ses chiffres. C’est-à-dire 2+0=2. Ecrire enfin ce chiffre à droite.
Règle de vérification
Si le chiffre écrit à droite est égal au chiffre écrit à gauche, alors le résultat est probablement correct. C’est le cas maintenant où les deux chiffres sont égaux à 2.
Si le chiffre écrit à droite est différent du chiffre écrit à gauche, alors le résultat est à 100% incorrect. Il faut alors chercher l’erreur au niveau de votre calcul de l’opération et ensuite revérifier.
Il est possible de vérifier de la même manière une opération d’addition, sauf qu’à la 3ème étape, il faut ajouter au lieu de multiplier les chiffres substituts des deux valeurs.
Soit par exemple l’opération :
7292 + 362 = 7654
En haut, c’est 2. J’ai ignoré le 9 et également le 7 avec le 2.
En bas, c’est 2. J’ai ignoré le 3 avec le 6.
A gauche, c’est 4. J’ai ignoré le 5 avec le 4. J’ai calculé 7+6=13. Et 1+3=4
A droite, c’est 2 + 2 = 4. C’est-à-dire la somme des chiffres substituts des deux valeurs.
Pour vérifier une opération de soustraction, je préfère toujours, vérifier l’opération d’addition correspondante.
L’équivalent de l’opération : 7 - 4 = 3, est l’opération d’addition : 7 = 4 + 3.
C’est-à-dire, la première valeur de l’opération de soustraction est la somme de la valeur retranchée et de la valeur résultat.
Une opération de division est vérifiée à l’aide de l’opération de multiplication correspondante.
L’équivalent de l’opération : 12 : 4 = 3, est l’opération de multiplication : 12 = 4 x 3.
C’est-à-dire, le dividende de l’opération de division est le produit du diviseur et du quotient.
Et en cas de reste de la division, il faut l’ajouter comme suit :
14 : 4 = 3 (r = 2) est équivalente à : 14 = (4 x 3) +2
Donc, pour vérifier une opération de division, il faut à la 3ème étape, multiplier le quotient par le diviseur et puis ajouter le reste.
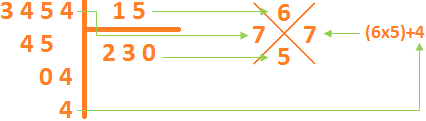
Donnons un exemple : 3454 : 15 = 230 et reste = 4.
En haut c’est la somme des chiffres du diviseur. C’est-à-dire 1+5=6.
En bas c’est la somme des chiffres du quotient. C’est-à-dire 2+3=5.
A gauche c’est la somme des chiffres du dividende. C’est-à-dire 3+4=7.
A droite c’est (5x6)+4=34. Et 3+4=7.
Nous avons le même chiffre à droite et à gauche. La vérification a pour résultat positif.
