6. La méthode japonaise de calcul de produit
La méthode japonaise de calcul de produits consiste à dessiner des traits et de compter les points d’intersections entre ces traits pour trouver le résultat.
Cette méthode est d’apparence magique. Mais, si nous l’étudions de près, nous apercevrons qu’elle est semblable à la méthode classique de calcul, sauf… sans utilisation des tables de multiplication.
Avant de décrire la méthode et de montrer sa similitude par rapport à la méthode classique de multiplication, je vous montre comment compter un produit de chiffres à l’aide de traits.
Compter un produit de chiffres à l’aide de traits
Les enfants commencent à compter les additions et soustractions à l’aide de leurs doigts ou à l’aide d’autres objets. Mais, à un certain niveau les tables d’addition doivent être connues par cœur.
Bien entendu, les tables de multiplication doivent également être connues par cœur. Je vous montre tout de même comment peut-on compter un produit de chiffres.
Soit par exemple : 6 x 4
Une première solution est de dessiner un rectangle avec 6 carreaux en longueur et 4 carreaux en largeur comme suit :

Comptez ensuite le nombre de carreaux. Vous trouverez 6 x 4 = 24.
Une autre solution est de dessiner 4 traits croisés avec 6 traits comme suit :

Compter ensuite le nombre des points d’intersections entre les traits dessinés.

Méthode japonaise de calcul de produits
1er exemple
Calculons par exemple : 41 x 23
Je commence par tracer des traits pour chaque chiffre en croisant les chiffres de la 1ère valeur avec ceux de la 2ème valeur, comme suit :
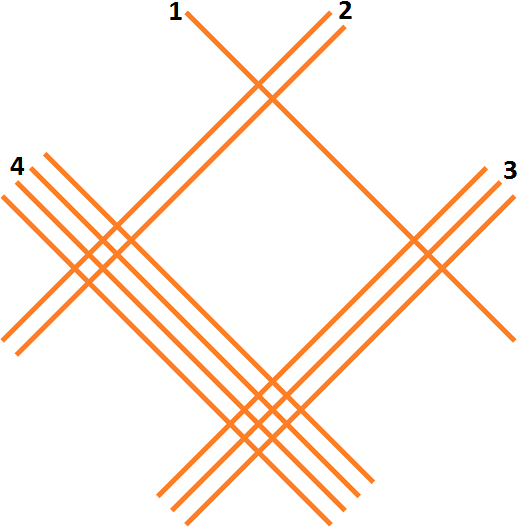
Ensuite, il faut regrouper les intersections entre les lignes des chiffres comme indiqué dans le schéma suivant. C’est-à-dire :
- 1er groupe : Intersections des traits correspondant au chiffre des unités de la 1ère valeur avec les traits correspondant au chiffre des unités de la 2ème valeur
- 2ème groupe : Intersections des traits correspondant au chiffre des unités de la 1ère valeur avec les traits correspondant au chiffre des dizaines de la 2ème valeur ET Intersections des traits correspondant au chiffre des dizaines de la 1ère valeur avec les traits correspondant au chiffre des unités de la 2ème valeur
- 3ème groupe : Intersections des traits correspondant au chiffre des dizaines de la 1ère valeur avec les traits correspondant au chiffre des dizaines de la 2ème valeur
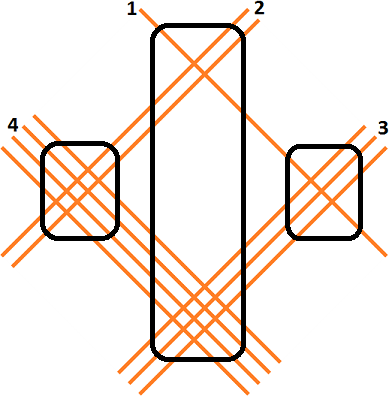
Je compte maintenant les points d’intersection au niveau du groupe 1. Je trouve le nombre 3 qui n’est rien d’autre que le produit des deux chiffres en unité à savoir 3 et 1.
Un premier chiffre du résultat est trouvé. Je pose 3 en case des unités.
![]()
Je compte ensuite les points d’intersection au niveau du groupe 2. Je trouve le nombre 14.
- En haut 2 qui est égal à 1x2 et
- En bas 12 qui est égal à 3x4.
Pour la valeur 14, je pose 4 en classe des dizaines du résultat, et je retiens 1.
![]()
En groupe 3, je commence à compter à partir de 2 afin de prendre en compte le 1 retenu du groupe 2. Je trouve le nombre 9. En effet, 1+(2x4)=9.
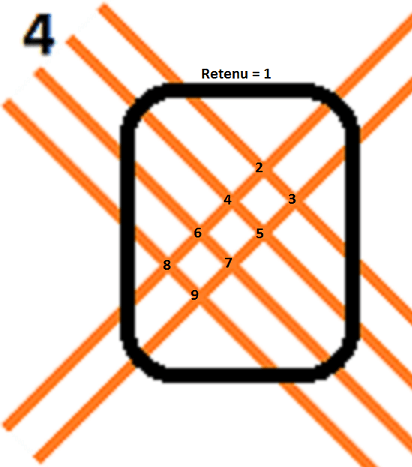
Le chiffre des centaines du résultat est 9. Le résultat de la multiplication de 41 x 23 est :
![]()
Calculons maintenant ce produit avec la méthode classique de calcul de multiplication, afin de voir sa similitude avec la méthode japonaise.
Nous commençons par multiplier 3 par 1 et c’est bien ce qui est retrouvé au groupe 1 et qui n’est rien d’autre que le produit de 1 par 3.

Ensuite, nous multiplions 3 par 4, nous obtenons 12. Cette valeur est comptée en bas du 2ème groupe. Et nous multiplions 2 par 1, nous obtenons 2. Cette valeur est comptée en haut du 2ème groupe. Nous obtenons donc 4 en dizaine avec 1 retenu pour la case des centaines.
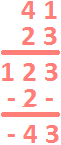
Ensuite, nous multiplions 2 par 4, nous obtenons 8 qui est ajouté à 1, retenu du 2ème groupe, pour trouver enfin 9 en classe des centaines.
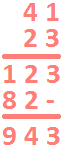
2ème exemple
Calculons par exemple : 463 x 507
Je commence par tracer les traits pour chaque chiffre comme suit :
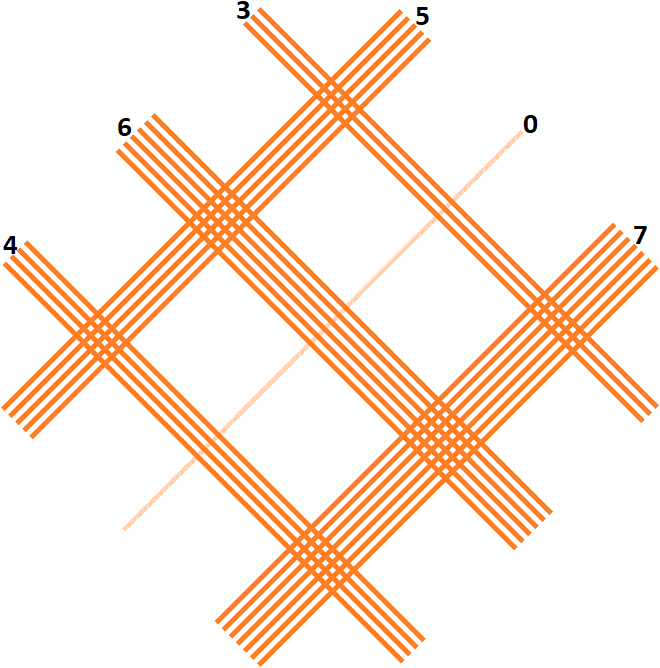
NB. Pour le chiffre 0, il faut tracer une ligne en pointillait ou avec une autre couleur. Le but est de ne pas compter ses intersections avec les lignes de l’autre valeur.
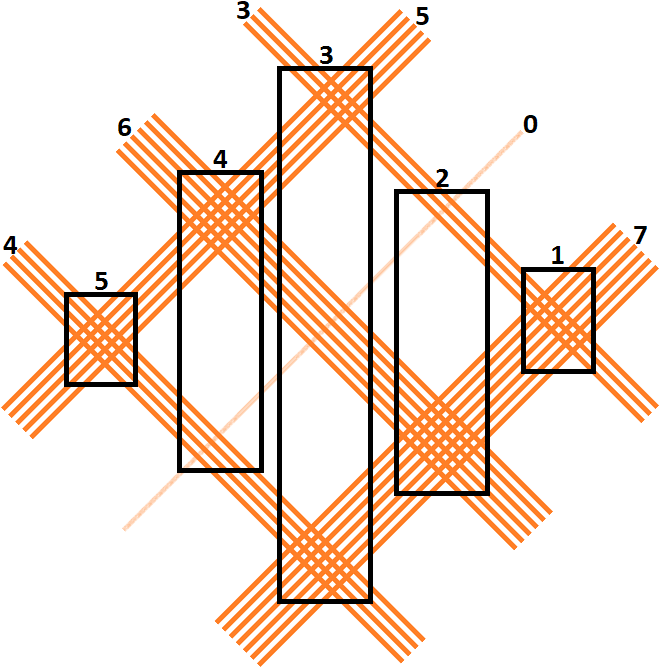
Ensuite, il faut regrouper les intersections entre les lignes des chiffres comme indiqué dans le schéma suivant. C’est-à-dire :
- 1er groupe : Unités-unités
- 2ème groupe : Unités-dizaines + dizaines-unités
- 3ème groupe : Unités-centaines + dizaines-dizaines + centaines-unités
- 4ème groupe : Dizaines-centaines + centaines-dizaines
- 5ème groupe : Centaines-centaines
Je compte maintenant les points d’intersection au niveau du groupe 1. Je trouve le nombre 21 qui n’est rien d’autre que le produit des deux chiffres en unité à savoir 3 et 7.
Un premier chiffre du résultat est trouvé. Je pose 1 en classe des unités et je retiens 2.
![]()
En groupe 2, je commence à compter à partir de 3 afin de prendre en compte le 2 retenu. Je trouve le nombre 44. En effet,
2+(6x7)+(0x3)= 44
Je rappelle qu’il ne faut pas compter les points d’intersection avec la ligne correspondante au chiffre 0.
Le chiffre des dizaines du résultat est 4, et je retiens 4.
![]()
En groupe 3, je commence à compter à partir de 5 afin de prendre en compte le 4 retenu. Je trouve le nombre 47. En effet,
4+(3x5)+(0x6)+(4x7)= 47
Le chiffre des centaines du résultat est 7, et je retiens 4.
![]()
En groupe 4, je commence à compter à partir de 5 afin de prendre en compte le 4 retenu. Je trouve le nombre 34. En effet,
4+(6x5)+(0x4)= 34
Le chiffre des milliers du résultat est 4, et je retiens 3.
![]()
En groupe 5, je commence à compter à partir de 4 afin de prendre en compte le 3 retenu. Je trouve le nombre 23. En effet,
3+(5x4)= 23
Le résultat est donc 234741.
![]()