5. Deuxième méthode de multiplication
La 2ème méthode de multiplication est basée sur l’égalité suivante :
a x b = (a + b – r) x r + (a – r) x (b – r)
ou bien
a x b = (a + b – r) x r + (r – a) x (r – b)
Cette méthode rend le calcul de multiplication facile notamment lorsque les deux valeurs à multiplier sont proches l’une de l’autre.
1er exemple
Soit l’exemple : 18 x 13
Je choisis pour la référence que j’ai représentée par « r » la valeur 10. Remarquez à quel point le calcul de cette multiplication est facile ?
| Je fais la somme | 18+13=31 | |
| Je retranche 10 | 31-10=21 | |
| Je multiplie par 10 | 21x10=210 | Je mémorise 210 |
| Je multiplie les écarts par rapport à 10 | 8x3=24 | j’ajoute 24 à 210, j’obtiens le résultat 234 |
Vous pouvez vérifier que 18 x 13 = 234.
NB. J’ai retranché la référence 10 en 2ème étape. Mais, dans le cas présent, vous pouvez bien commencer par retrancher la référence 10 de l’une des deux valeurs et ensuite ajouter le reste à l’autre valeur. Par exemple, 18-10=8, puis ajouter 8+13=21. Cela facilite un peu plus le calcul. Par contre, dans le cas de l’exemple suivant où les deux valeurs sont inférieures à la référence, il convient d’ajouter d’abord les deux valeurs et ensuite retrancher la référence du résultat.
2ème exemple
Soit l’exemple : 8 x 6
C’est 48 ; ça doit être appris par cœur. Mais, appliquons la méthode décrite plus haut en utilisant toujours la référence 10.
C’est utile pour comprendre la méthode et également un secours si on a pas bien appris toutes les tables de multiplication.
| Je fais la somme | 8+6=14 | |
| Je retranche 10 | 14-10=4 | |
| Je multiplie par 10 | 4x10=40 | Je mémorise 40 |
| Je multiplie les écarts par rapport à 10 | 2x4=8 | J’ajoute 8 à 40, j’obtiens le résultat 48 |
Ouvrons maintenant une parenthèse. Des gens utilisent leurs doigts pour trouver les produits des nombres entre 6 et 9. Cette manière de compter avec les doigts est expliquable par la méthode que nous sommes en train d’étudier en cette rubrique.
Je décris cette manière d’utilisation des doigts en prenant le même exemple : 6x8 :
1ère règle : les doigts des deux mains sont numérotés du petit auriculaire au pouce avec les valeurs 6 à 10.

2ème règle : pour calculer 6x8, je dois mettre le doigt n° 6 (qui est le petit auriculaire) de la main gauche en face du doigt n°8 (qui est le majeur) de la main droite. Et j'imagine une ligne tracée juste au dessus de ces deux doigts
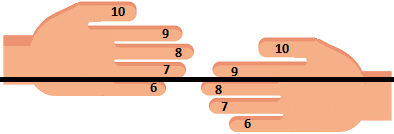
3ème règle : Je compte les doigts en bas de cette ligne et c’est le chiffre de dizaines. Il s’agit de 1+3=4 dans notre cas.
NB. Remarquez que cela est équivalent à 6-5+8-5 qui est égale à 6+8-10. Donc, nous retrouvons la formule montrée plus haut.
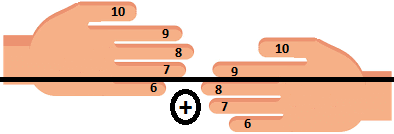
4ème règle : je compte les doigts en haut de la ligne pour chaque main et je les multiplie pour trouver le chiffre d’unités. Il s’agit de 4x2=8 dans notre cas.
NB. Remarquez que cela est équivalent à (10-6)x(10-8). Donc, nous retrouvons toujours la formule utilisée pour notre méthode.
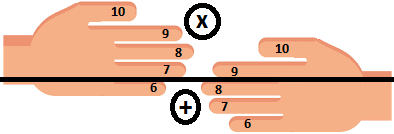
3ème exemple
Soit l’exemple : 16 x 7
Ici encore, nous allons utilisez la référence 10. Mais remarquez qu’une valeur est supérieure à 10 tandis que l’autre est inférieure à 10. Lorsque c’est le cas, il faut retrancher le produit des écarts par rapport à la référence 10 et non pas l’ajouter.
| Je fais la somme | 16+7=23 | |
| Je retranche 10 | 23-10=13 | |
| Je multiplie par 10 | 13x10=130 | Je mémorise 130 |
| Je multiplie les écarts par rapport à 10 | 6x3=18 | Je retranche 18 de 130, j’obtiens le résultat 112 |
Exemple avec 100 comme référence
Soit l’exemple : 94 x 109
Les deux valeurs de l’opération sont proches de 100 ; utilisons 100 comme référence :
| Je fais la somme |
94+109 |
|
| Je retranche 100 | 203-100 =103 |
|
| Je multiplie par 100 |
103x100 |
Je mémorise 10300 |
| Je multiplie les écarts par rapport à 100 | 6x9=54 | Je retranche 54 de 10300, j’obtiens le résultat 10246 |
Exemple avec 20 comme référence
Soit l’exemple : 23 x 29
Utilisons 20 comme référence :
| Je fais la somme | 23+29=52 | |
| Je retranche 20 | 52-20=32 | |
| Je multiplie par 20 | 32x20 =32x2x10 =640 |
Je mémorise 640 |
| Je multiplie les écarts par rapport à 20 | 3x9=27 | J’ajoute 27 à 640, j’obtiens le résultat 667 |
Autre exemple : 31 x 56
1ère solution
Utilisons 40 comme référence :
| Je fais la somme | 31+56=87 | |
| Je retranche 40 | 87-40=47 | |
| Je multiplie par 40 |
47x40 |
Je mémorise 1880 |
| Je multiplie les écarts par rapport à 40 |
9x16 |
Je retranche 144 de 1880, j’obtiens le résultat 1736 |
2ème solution
31 x 56 = 31 x 28 x 2
Nous pouvons faciliter cette opération en calculons d’abord 31 x 28 et ensuite multiplier le résultat par 2
Pour le calcul 31 x 28, utilisons 30 comme référence :
| Je fais la somme | 31+28=59 | |
| Je retranche 30 | 59-30=29 | |
| Je multiplie par 30 | 29x30 =(30x30)-30 =900-30 =870 |
Je mémorise 870 |
| Je multiplie les écarts par rapport à 30 | 1x2=2 | Je retranche 2 de 870, j’obtiens le résultat 868 |
Je multiplie ensuite 868 par 2, et j'obtiens le résultat :
31 x 56 = 1736
Exemple avec double utilisation de la méthode
Soit l’exemple : 144 x 123
Utilisons 100 comme référence :
| Je fais la somme | 144+123=267 | |
| Je retranche 100 | 267-100=167 | |
| Je multiplie par 100 | 167x100 =16700 |
Je mémorise 16700 |
| Je multiplie les écarts par rapport à 100 | 44x23 =22x23x2 |
??? |
Je vais réappliquer la méthode en utilisant la référence 20 pour calculer 22 x 23. Je multiplie ensuite le résultat par 2.
| Je fais la somme | 22+23=45 | |
| Je retranche 20 | 45-20=25 | |
| Je multiplie par 20 |
25x20 |
Je mémorise 500 |
| Je multiplie les écarts par rapport à 20 | 2x3=6 | J’ajoute 6 à 500, j’obtiens le résultat 506 |
44 x 23 = 22 x 23 x 2 = 506 x 2 = 1012
Une parenthèse : le calcul de 44 x 23 peut être fait d’une autre manière si je remarque que 44=11x4 :
23 x 44 = 23 x 11 x 2 x 2 = 253 x 2 x 2 = 506 x 2 = 1012
Revenons à notre problème principal. J’ai mémorisé 16700, je dois lui ajouter 1012. Le résultat est :
144 x 123 = 17712
Cas particuliers
Produit de 2 valeurs ayant le même nombre de dizaines et dont les chiffres d’unités se complémentent à 10
Pour calculer le produit de 2 valeurs ayant le même nombre de dizaines et dont les chiffres d’unités se complémentent à 10 :
- Multiplier le chiffre de dizaines par le chiffre suivant et metre le résultat en centaines
- Calculer le produit des chiffres d’unités et l’ajouter au résultat précédent
Exemple 67 x 63 :
- Calculer 6 x 7 = 42, je mémorise 4 200
- Calculer 7 x 3 = 21. J’ajoute 21 à 4 200. Le résultat est 4 221
NB. Il s’agit d’un cas particulier d’utilisation de la méthode étudiée en cette rubrique.
Carré d’un nombre dont le chiffre d’unités est 5
Pour calculer le carré d’un nombre dont le chiffre d’unités est 5 :
- Multiplier le chiffre de dizaines par le chiffre suivant et mettre le résultat en centaines
- Ajouter 25 au résultat précédent
Exemple : 352
- Calculer 3 x 4 = 12,
- Le résultat est 1225.
Lorsque les deux valeurs ne sont pas proches l’une de l’autre
Il est possible d’utiliser la méthode lorsque les deux valeurs à multiplier ne sont pas proches l’une de l’autre, mais en utilisant deux références :
Si une référence est un multiple de l’autre, utilisez la formule :
a x b = (k x a + b - k x r) x r + (a – r) x (b – k x r)
Si les deux références sont multiples d’une même valeur, utilisez la formule :
a x b = (l x a + b x k – k x l x r) x r + (a – k x r) * (b – l x r)
Exemple : 43 x 18
J’utilise comme références 40 et 20. 40 est multiple de 20. J’utilise donc la 1ère formule avec k=2 (car 40=20x2)
| Je fais la somme de 43 et 18x2 (*) |
43+(18x2) |
|
| Je retranche 40 (**) | 79-40=39 | |
| Je multiplie par 20 (***) | 39x20 =(40x20)-20 = 800-20 =780 |
Je mémorise 780 |
| Je multiplie les écarts par rapport aux références | 3x2=6 | Je retranche 6 de 780, j’obtiens le résultat 774 (****) |
(*) J'ai multiplié la petite valeur avec le facteur k
(**) J'ai retranché la référence supérieure
(***) J'ai multiplié par la référence inférieure
(****) J’ai retranché car 43 est supérieure à sa référence 40 et 18 est inférieure à sa référence 20.
Exemple : 52 x 34
J’utilise comme références 50 et 30. 50 et 30 sont multiple de 10 avec comme facteurs k=5 et l=3
| Je fais la somme de 52x3 et 34x5 (*) | (52x3)+(34x5) =156+170 = 326 |
|
| Je retranche 10x3x5 (**) | 326-150=176 | |
| Je multiplie par 10 (***) | 176x10=1760 | Je mémorise 1760 |
| Je multiplie les écarts par rapport aux références | 2x4=8 | J’ajoute 8 à 1760, j’obtiens le résultat 1768 |
(*) J'ai multiplié les valeurs avec les facteurs de manière croisée
(**) J'ai retranché le diviseur commun des deux références multiplié par les deux facteurs
(***) J'ai multiplié par 10 qui est le diviseur commun des deux références.