4. Première méthode de multiplication
La 1ère méthode de multiplication est basée sur les égalités :
(b + c) x a = (b x a) + (c x a)
(b + c) / a = (b / a) + (c / a)
a x (b + c) = (a x b) + (a x c)
et
(a + b) x (c + d) = (a x c) + (a x d) + (b x c) + (b x d)
Ainsi que les identités remarquables
(a + b)2 = a2 + 2 x a x b + b2
(a - b)2 = a2 - 2 x a x b + b2
(a + b) x (a – b) = a2 - b2
Utilisation des 1ères égalités
Calculer : 36 x 7
Pour cela, il convient de décomposer 36 en 30 et 6.
| 36 x 7 | = (30 + 6) x 7 |
| = 30 x 7 + 6 x 7 | |
| = 210 + 42 | |
| = 252 |
Calculer : 45 x 19
| 45 x 19 | = 45 x (20 - 1) |
| = 45 x 20 - 20 | |
| = 900 - 45 | |
| = 855 |
Calculer : 58 / 2
| 58 / 2 | = (60 - 2) / 2 |
| = (60 / 2) - (2 / 2) | |
| = 30 - 1 | |
| = 29 |
Calculer : 134 / 2
| 134 / 2 | = (120 + 14) / 2 |
| = (120 / 2) + (14 / 2) | |
| = 60 + 7 | |
| = 67 |
Calculer : 522 / 3
Je décompose 522 en 300 et 222 et puis 222 en 210 et 12.
| 522 / 3 | = (300 + 210 + 12) / 3 |
| = (300 / 3) + (210 / 3) + (12 / 3) | |
| = 100 + 70 + 4 | |
| = 174 |
522 / 3 = (300 + 210 + 12) / 3 = (300 / 3) + (210 / 3) + (12 / 3) = 100 + 70 + 4 = 174
Utilisation de l’égalité (a + b) x (c + d) = (a x c) + (a x d) + (b x c) + (b x d)
Soit par exemple : 54 x 38 :
| 54 x 38 | = (50 + 4) x (30 + 8) |
| = (50 x 30) + (50 x 8) + (4 x 30) + (4 x 8) |
|
| = 1500 + 400 + 120 + 32 | |
| = 1532 + 520 | |
| = 2052 |
En calcul mental, nous procédons ainsi :
1 - Je multiplie les dizaines 5x3=15
Je mémorize 15 (1 en milliers et 5 en centaines)
![]()
2 - Je multiplie les unités 4x8=32
j’ajoute 32 ce qui donne 1532
![]()
3 - Je multiplie diagonalement 5x8=40 et 4x3=12
j’additionne 40+12=52 que je mets en centaines et dizaines : 5 en centaines et 2 en dizaines
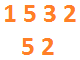
4 - Je calcule la somme 1532+520=2052 et c’est le résultat.
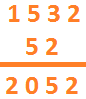
Autre exemple : 68 x 47 :
| 68 x 47 | = (70 - 2) x (50 - 3) |
| = (70 x 50) - (70 x 3) - (2 x 50) + (2 x 3) |
|
| = 3500 - 210 - 100 + 6 | |
| = 3506 - 310 | |
| = 3506 - 306 - 4 | |
| = 3200 - 4 | |
| = 3196 |
Utilisation d’identités remarquables
(a + b)2 = a2 + 2 x a x b + b2
(a - b)2 = a2 - 2 x a x b + b2
(a + b) x (a – b) = a2 - b2
Exemple: 34 x 34
| 34 x 34 | = (30 + 4)2 |
| =302 + 2 x 30 x 4 + 42 | |
| = 900 + 16 + 240 | |
| = 1156 |
Exemple 45 x 45
Utilisons pour cela l’identité :
a2 – b2 = (a + b) x (a – b)
| 452 - 52 | = (45 + 5) x (45 - 5) |
| 45 x 45 - 25 | = 50 x 40 |
| 45 x 45 | = 2000 + 25 |
| = 2025 |
Autre exemple d’utilisation de cette formule.
a2 – b2 = (a + b) x (a – b)
Calculez : 56 x 64
Remarquez que l’écart des deux valeurs par rapport à 60 est 4.
| 56 x 64 | = (60 - 4) x (60 + 4) |
| = 602 - 42 | |
| = 3600 - 16 | |
| = 3584 |