البكالوريا تمارين اللوغاريتم للأساس a

راجع الدرس اللوغاريتم للأساس a

تمرين 1

حل في ℝ المعادلات التالية

1. log(x - 2) = log(3)
2. log(x - 5) - log(3x + 1) = 0
3. log(3x - 1) = 3

تصحيح

1 - المعادلة

log(x - 2) = log(3)

المعادلة معرفة إذا كان

x - 2 > 0 ⇒ x > 2

المعادلة معرفة على ]2;+∞[

و حيث أن

5 ∈ ]2;+∞[

مجموعة الحلول للمعادلة هي S = {5}

2 - المعادلة

log(x - 5) - log(3x + 1) = 0

المعادلة معرفة إذا كان

x - 5 > 0 ⇒ x > 5
و
3x + 1 > 0 ⇒ x > -1 / 3

المعادلة معرفة على ]5;+∞[

و حيث أن

-3 ∈ ]5;+∞[

مجموعة الحلول للمعادلة هي S = {-3}

3 - المعادلة

log(3x - 1) = 3

المعادلة معرفة إذا كان

3x - 1 > 0 ⇒ x > 1 / 3

المعادلة معرفة على ] 1 / 3 ;+∞[

و حيث أن

333 ∈ ] 1 / 3 ;+∞[

مجموعة الحلول للمعادلة هي S = {333}

تمرين 2

حل في ℝ المتراجحات التالية

1. log(x - 3) - log(x + 1) > 1
2. log(3x - 2) - log(x + 1) > log(2x - 3) - log(x + 4)
3. log(x - 2) + log(2x - 1) < log(x² - 3x + 2)

تصحيح

1 - المتراجحة

log(x - 3) - log(x + 1) > 1

المتراجحة معرفة إذا كان

x - 3 > 0 ⇒ x > 3
و
x + 1 > 0 ⇒ x > -1

المتراجحة معرفة على ]3;+∞[

مجموعة الحلول للمتراجحة هي S = ]3;+∞[∩] -13 / 9 ;+∞[ = ]3;+∞[

2 - المتراجحة

log(3x - 2) - log(x + 1) > log(2x - 3) - log(x + 4)

المتراجحة معرفة إذا كان

3x - 2 > 0 ⇒ x > 2 / 3
و
x + 1 > 0 ⇒ x > -1
و
2x - 3 > 0 ⇒ x > 3 / 2
و
x + 4 > 0 ⇒ x > -4

المتراجحة معرفة على ] 3 / 2 ;+∞[

لدينا متراجحة من الدرجة التانية. المميز

Δ = 141

النقط حيث تنعدم كثيرة الحدود

x₁ = -11 - √141 / 2 ≃ -11,44
x₂ = -11 + √141 / 2 ≃ 0,44

كثيرة الحدود موجبة إذا كان

x ∈ ]-∞; -11 - √141 / 2 [U] -11 + √141 / 2 ;+∞[

مجموعة الحلول للمتراجحة هي S = ] 3 / 2 ;+∞[∩(]-∞; -11 - √141 / 2 [U] -11 + √141 / 2 ;+∞[) = ] 3 / 2 ;+∞[

3 - المتراجحة

log(x - 2) + log(2x - 1) < log(x² - 3x + 2)

نلاحظ أن

x² - 3x + 2 = (x - 1)(x - 2)

المتراجحة معرفة إذا كان

x - 2 > 0 ⇒ x > 2
و
2x - 1 > 0 ⇒ x > 1 / 2
و
(x - 1)(x - 2) > 0 ⇒ x < 1 ou x > 2

المتراجحة معرفة على ]2;+∞[

مجموعة الحلول للمتراجحة هي S = ]2;+∞[∩]-∞;0[ = ∅

تمرين 3

دراسة الدالة f المعرَّفة على ]0;+∞[ ب :

f(x) = x - log(x)

1. احسب النهايات في 0 و +∞ ل f(x).
2. احسب f '(x).
3. ادرس إشارة f '(x) و أنشئ جدول التغيرات للدالة
4. احسب f "(x).
5. ادرس إشارة f "(x). استنتج أن مبيان الدالة Cf محدَّب على مجموعة تعريف الدالة f.
6. احسب النهاية في +∞ ل f(x) / x و f(x) - x. استنتج.
7. ارسم المبيان Cf.

تصحيح

1 - النهايات في 0 و +∞ ل f(x)

lim x→0 x > 0 f(x) = lim x→0 x > 0 (x - log(x)) = +∞

lim x→+∞ f(x) = lim x→+∞ (x - log(x)) = lim x→+∞ (x(1 - log(x) / x )) = +∞

2 - حساب f '(x)

f '(x) = 1 - 1 / ln(10) . x

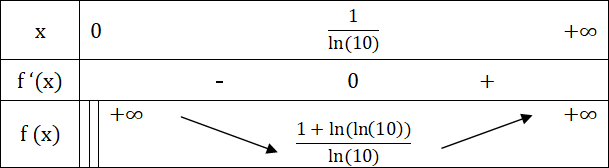
3 - إشارة f '(x) و جدول التغيرات

f '(x) > 0 ⇒ 1 - 1 / ln(10) . x > 0 ⇒ 1 > 1 / ln(10) . x ⇒ x > 1 / ln(10)

حساب f( 1 / ln(10) ).

f( 1 / ln(10) ) = 1 / ln(10) - log( 1 / ln(10) ) = 1 / ln(10) + log(ln(10)) = 1 + ln(ln(10)) / ln(10)

جدول التغيرات كما يلي :

4 - حساب f "(x)

f "(x) = 1 / ln(10) . x²

5 - إشارة f "(x) و تحدب و تقعر Cf

10 > 1 ⇒ ln(10) > 0 ⇒ f "(x) > 2

f "(x) دائما موجبة. إذن مبيان الدالة Cf محدَّب على مجموعة تعريف الدالة f.

6 - الفروع اللانهائية

lim x→+∞ f(x) / x = lim x→+∞ 1 + log(x) / x = 1

lim x→+∞ (f(x) - x) = lim x→+∞ (- log(x)) = -∞

يقبل مبيان الدالة بجوار +∞ فرعا شلجميا اتجاهه المستقيم الذي معادلته y = x.

7 - المبيان Cf

<< 6. البكالوريا اللوغاريتم للأساس a

8. البكالوريا خصائص الدالة الأسية الطبيعية >>