البكالوريا اللوغاريتم للأساس a
تعريف
دالة اللوغاريتم للأساس a (a ∈ ℝ+-{1})، و تكتب loga، معرفة على ]0;+∞[ ب
loga(x) = ln(x) ln(a)
دالة اللوغاريتم الطبيعي هي دالة اللوغاريتم ذات الأساس e، لأن ln(e) = 1.
مثال
يستخدم بالأساس اللوغاريتم للأساس 10، المعروف باسم اللوغاريتم العشري و الذي نرمز له ب. log10 أو log.
الدالة log هي الدالة العكسية للدالة أس 10. أي الدالة المُعرَّفة بـ 10x.
log(10) = 1
log(1 000) = 3
log(0,01) = -2
خصائص
من المهم معرفة أن ∀ a ∈ ℝ-{1} :
loga(1) = 0
loga(a) = 1
دالة اللوغاريتم للأساس a
- تصاعدية قطعا على المجال ]0;+∞[ في حالة a > 1.
- تنازلية قطعا على المجال ]0;+∞[ في حالة a < 1.
إذن
x = y ⇔ loga(x) = loga(y)
في حالة a > 1 فإن 0 < x < y ⇔ loga(x) < loga(y)
في حالة a < 1 فإن 0 < x < y ⇔ loga(x) > loga(y)
إذن
x = 1 ⇔ loga(x) = 0
في حالة a > 1 فإن 0 < x < 1 ⇔ loga(x) < 0
و x > 1 ⇔ loga(x) > 0
في حالة a < 1 فإن 0 < x < 1 ⇔ loga(x) > 0
و x > 1 ⇔ loga(x) < 0
خصائص أخرى
loga(xy) = loga(x) + loga(y)
loga(
1
x
) = -loga(x)
loga(
x
y
) = loga(x) - loga(y)
loga(xn) = n loga(x)
loga(√x) =
1
2
loga(x)
أمثلة
احسب
log(1 000) + 3 log(100) - 4 log(0,01)
حل المعادلة
log(x + 1) = log(4 - x)
المعادلة معرفة إذا كان
x + 1 > 0 ⇒ x > -1
و
4 - x > 0 ⇒ x < 4
المعادلة معرفة على ]-1;4[
و حيث أن
3 2 ∈ ]-1;4[
مجموعة الحلول للمعادلة هي S = { 3 2 }
النهايات الاعتيادية
النهايات على يمين 0
lim
x→0
x > 0
loga(x) = -∞ في حالة a > 1
و
lim
x→0
x > 0
loga(x) = +∞ في حالة a < 1
lim x→0 x > 0 xn loga(x) = 0 (n ∈ ℕ*)
النهايات في +∞
lim
x→+∞
loga(x) = +∞ في حالة a > 1
و
lim
x→+∞
loga(x) = -∞ في حالة a < 1
lim x→+∞ loga(x) xn = 0 (n ∈ ℕ*)
النهايات في 1
lim x→1 loga(x) x - 1 = 1 ln(a)
ملحوظة. هذه النهاية هي ببساطة مشتقة دالة اللوغاريتم للأساس a في 1.
هناك أيضًا متغير لهذه النهاية يمكن استنتاجه ببساطة عن طريق تغيير المتغير : :
lim x→0 loga(x + 1) x = 1 ln(a)
الدالة المشتقة لدالة اللوغاريتم للأساس a
الدالة المشتقة لدالة اللوغاريتم للأساس a هي الدالة المعرفة على ]0;+∞[ ب
f(x) = 1 ln(a) x
(loga(u(x))) ' = u '(x) ln(a) u(x)
مثال
لنحسب الدالة المشتقة للدالة f المعرَّفة بـ
f(x) = log(x2 + 2x + 2)
f '(x) = (x2 + 2x + 2) ' ln(10) log(x2 + 2x + 2) = 2x + 2 ln(10) log(x2 + 2x + 2)
الفروع اللانهائية
لقد رأينا النهاية على يمين 0
lim
x→0
x > 0
loga(x) = -∞ في حالة a > 1
و
lim
x→0
x > 0
loga(x) = +∞ في حالة a < 1
يقبل مبيان دالة اللوغاريتم للأساس a فرعا شلجميا رأسيا معادلته x = 0 (محور الأراتيب).
فيما يتعلق بالنهايات بجوار +∞
lim
x→+∞
loga(x) = +∞ في حالة a > 1
و
lim
x→+∞
loga(x) = -∞ في حالة a < 1
lim x→+∞ loga(x) x = 0
يقبل مبيان دالة اللوغاريتم للأساس a بجوار +∞ فرعا شلجميا اتجاهه محور الأفاصيل.
جدول التغيرات
في حالة a > 1، جدول التغيرات لدالة اللوغاريتم للأساس a كما يلي :

في حالة a < 1، جدول التغيرات لدالة اللوغاريتم للأساس a كما يلي :
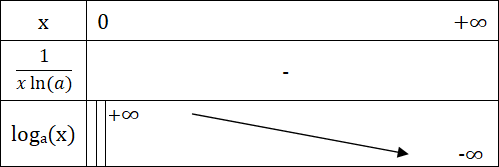
التمثيل المبياني لدالة اللوغاريتم للأساس a
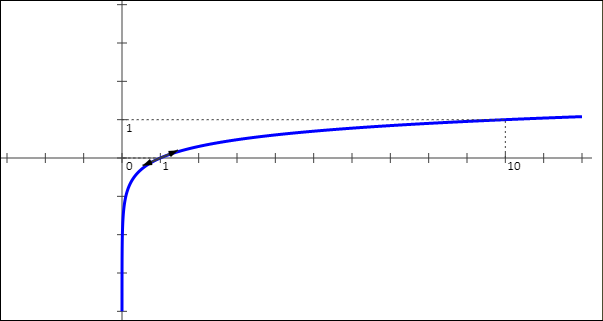
في حالة a > 1، التمثيل المبياني لدالة اللوغاريتم للأساس a كما يلي (ممثل اللوغاريتم للأساس 10) :
في حالة a < 1، التمثيل المبياني لدالة اللوغاريتم للأساس a كما يلي (ممثل اللوغاريتم للأساس 0.1) :
