البكالوريا الدالة الأسية للأساس a
تعريف
الدالة الأسية للأساس a (a ∈ ℝ+-{1})، و تكتب expa، معرفة على ℝ ب
expa(x) = ax = ex ln(a)
الدالة الأسية الطبيعية هي الدالة الأسية ذات الأساس e، لأن ln(e) = 1.
مثال
تستخدم بالأساس الدالة الأسية للأساس 10 وهي الدالة أس 10. أي الدالة المعرَّفة ب 10x.
101 = 10
103 = 1 000
10-2 = 0,01
خصائص
نجد الخصائص نفسها المعروفة للقوى :
expa(0) = a0 = 1
expa(1) = a1 = a
الدالة الأسية للأساس a
- تصاعدية قطعا على المجموعة ℝ في حالة a > 1.
- تنازلية قطعا على المجموعة ℝ في حالة a < 1.
إذن
x = y ⇔ ax = ay
في حالة a > 1 فإن 0 < x < y ⇔ ax < ay
في حالة a < 1 فإن 0 < x < y ⇔ ax > ay
و
x = 1 ⇔ ax = 0
في حالة a > 1 فإن 0 < x < 1 ⇔ ax < 0
و x > 1 ⇔ ax > 0
في حالة a < 1 فإن 0 < x < 1 ⇔ ax > 0
و x > 1 ⇔ ax < 0
خصائص أخرى
ax+y = ax . ay
a-x =
1
ax
ax-y =
ax
ay
(ax)y = ax y
(a . b)x = ax . bx
أمثلة
احسب
1 000 1003 . (0,01)4
حل المعادلة
ex + 1 = e4 - x
مجموعة الحلول للمعادلة هي S = { 3 2 }
النهايات الاعتيادية
النهايات في -∞
في حالة a > 1
lim x→-∞ ax = 0
lim x→-∞ xn ax = 0 (n ∈ ℕ*)
في حالة 0 < a < 1
lim x→-∞ ax = +∞
lim
x→-∞
ax
xn
= -∞ (n ∈ ℕ* فردي)
et
lim
x→-∞
ax
xn
= +∞ (n ∈ ℕ* زوجي)
النهايات في +∞
في حالة a > 1
lim x→+∞ ax = +∞
lim x→+∞ ax xn = +∞ (n ∈ ℕ*)
في حالة 0 < a < 1
lim x→+∞ ax = 0
lim x→+∞ xn ax = 0 (n ∈ ℕ*)
النهايات في 0
lim x→0 ax - 1 x = ln(a)
ملحوظة. هذه النهاية هي ببساطة مشتقة الدالة الأسية للأساس a في 0.
الدالة المشتقة للدالة الأسية للأساس a
الدالة المشتقة للدالة الأسية للأساس a هي الدالة المعرفة على ℝ ب
f(x) = ln(a) ax
(au(x)) ' = u '(x) ln(a) au(x)
مثال
لنحسب مشتقة الدالة f المعرَّفة بـ
f(x) = 10x2 + 2x + 2
f '(x) = (x2 + 2x + 2) ' ln(10) 10x2 + 2x + 2 = (2x + 2) ln(10) 10x2 + 2x + 2
الفروع اللانهائية
في حالة a > 1
النهاية بجوار -∞
lim x→-∞ ax = 0
يقبل مبيان الدالة الأسية للأساس a فرعا شلجميا أفقيا معادلته y = 0 (محور الأفاصيل).
النهايات بجوار +∞
lim x→+∞ ax = +∞
lim x→+∞ ax x = +∞
يقبل مبيان الدالة الأسية للأساس a بجوار +∞ فرعا شلجميا اتجاهه محور الأراتيب.
في حالة 0 < a < 1
النهاية بجوار +∞
lim x→+∞ ax = 0
يقبل مبيان الدالة الأسية للأساس a فرعا شلجميا أفقيا معادلته y = 0 (محور الأفاصيل).
النهايات بجوار -∞
lim x→-∞ ax = +∞
lim x→-∞ ax x = -∞
يقبل مبيان الدالة الأسية للأساس a بجوار -∞ فرعا شلجميا اتجاهه محور الأراتيب.
جدول التغيرات
في حالة a > 1، جدول التغيرات للدالة الأسية للأساس a كما يلي :
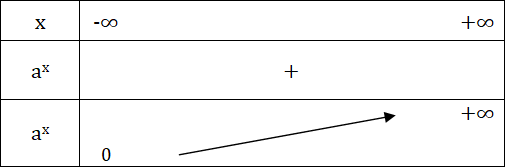
في حالة a < 1، جدول التغيرات للدالة الأسية للأساس a كما يلي :
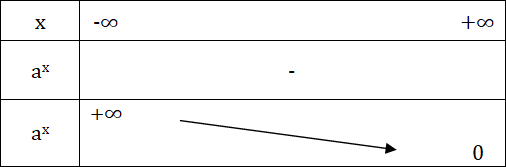
مبيان الدالة الأسية للأساس a
في حالة a > 1، التمثيل المبياني للدالة الأسية للأساس a كما يلي (ممثل الدالة الأسية للأساس 10) :

في حالة a < 1، التمثيل المبياني للدالة الأسية للأساس a كما يلي (ممثل الدالة الأسية للأساس 0.1) :
