Baccalauréat Calcul Intégral
Définition
Soient f une fonction continue sur un intervalle [a ; b] et F une primitive de f.
L'intégrale de f de a à b que l'on note ∫ a b f(x) dx est égal à F(b) - F(a).
On écrit :
∫ a b f(x) dx = [ F(x) ] a b = F(b) - F(a)
Exemple
Calcul des intégrales :
Propriété
Soit f une fonction continue sur un intervalle [a ; b].
Si f(x) > 0 sur [a ; b] alors ∫ a b f(x) dx > 0.
Si f(x) < 0 sur [a ; b] alors ∫ a b f(x) dx < 0.
Intégration par parties
Soient u et v deux fonctions continues sur un intervalle [a ; b] tel que leurs fonction dérivées u ' et v ' sont continues sur [a ; b]. Alors
∫ a b (u(x).v '(x)) dx = [ u(x).v(x) ] a b - ∫ a b (u '(x).v(x)) dx.
Exemple 1
Calcul de l'intégrale :
I = ∫ 1 2 x ex dx
On pose :
u(x) = x ⇒ u '(x) = 1
et
v '(x) = ex ⇒ v(x) = ex
Donc
Exemple 2
Calcul de l'intégrale :
I = ∫ 1 2 x2 ln(x) dx
On pose :
u(x) = ln(x) ⇒ u '(x) = 1 x
et
v '(x) = x2 ⇒ v(x) = 1 3 x3
Donc
Exemple 3
Calcul de l'intégrale :
I = ∫ 0 2 x √x + 1 dx
On pose :
u(x) = x ⇒ u '(x) = 1
et
v '(x) = 1 √x + 1 ⇒ v(x) = 2 √x + 1
Donc
Calcul d'aire à l'aide d'intégrale
Soit f une fonction continue sur un intervalle [a ; b].
L'aire délimitée par la courbe représentative de f, les droites d'équations x=a et x=b et l'axe des abscisses est égale à ∫ a b |f(x)| dx.
Donc
Si f(x) > 0 sur [a ; b] alors cette aire est égale à ∫ a b f(x) dx.
Si f(x) < 0 sur [a ; b] alors cette aire est égale à - ∫ a b f(x) dx.
Exemple
Soit f la fonction définie par :
f(x) = x2 - x - 2
Calculons l'aire délimitée par la courbe représentative de f, les droites d'équations x=1 et x=2 et l'axe des abscisses.
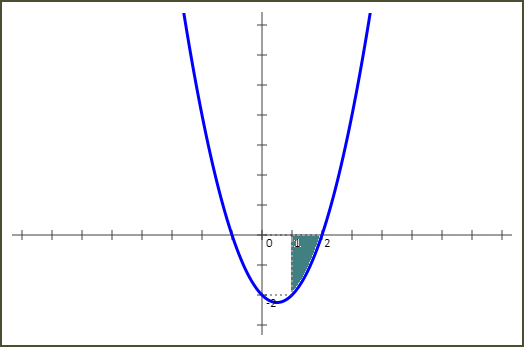
f(x) est négative sur l'intervalle [1 ; 2]. Donc l'aire demandée est égale à :
Calculons l'aire délimitée par la courbe représentative de f, les droites d'équations x=1 et x=3 et l'axe des abscisses.
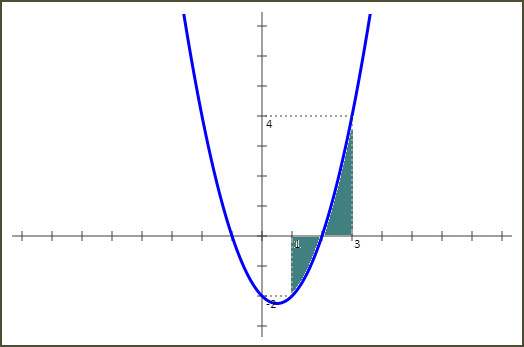
f(x) est négative sur l'intervalle [1 ; 2] et positive sur l'intervalle [2 ; 3]. Donc l'aire demandée est égale à :
Aire délimitée par une courbe et une droite
Soient f une fonction continue sur un intervalle [a ; b] et D une droite d'équation y = ax + b.
L'aire délimitée par la courbe représentative de f, les droites d'équations x=a et x=b et la droite D est égale à ∫ a b |f(x) - y| dx.
Donc
Si Cf est au dessus de D sur [a ; b] (cad f(x) > y) alors cette aire est égale à ∫ a b (f(x) - y) dx.
Si Cf est au dessous de D sur [a ; b] (cad f(x) < y) alors cette aire est égale à - ∫ a b (f(x) - y) dx.
Exemple
Soit f la fonction définie par :
f(x) = x2 - x - 2
Soit la droite D d'équation :
y = 2x - 8
Calculons l'aire délimitée par la courbe représentative de f, les droites d'équations x=-3 et x=-2 et la droite D.
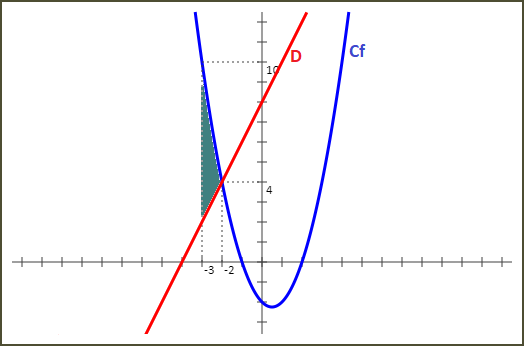
Cf est au dessus de D sur l'intervalle [1 ; 2]. Donc l'aire demandée est égale à :
Calculons l'aire délimitée par la courbe représentative de f, les droites d'équations x=-3 et x=0 et la droite D.
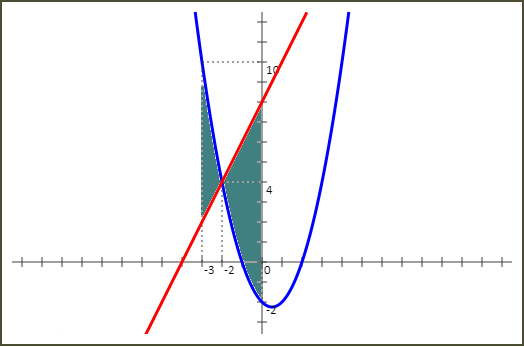
Cf est au dessus de D sur l'intervalle [-3 ; -2] et au dessous de D sur l'intervalle [-2 ; 0]. Donc l'aire demandée est égale à :
Aire délimitée par les courbes de deux fonctions
Soient f et g deux fonctions continues sur un intervalle [a ; b].
L'aire délimitée par la courbe représentative de f, les droites d'équations x=a et x=b et la courbe représentative de g est égale à ∫ a b |f(x) - g(x)| dx.
Donc
Si Cf est au dessus de Cg sur [a ; b] (cad f(x) > g(x)) alors cette aire est égale à ∫ a b (f(x) - g(x)) dx.
Si Cf est au dessous de Cg sur [a ; b] (cad f(x) < g(x)) alors cette aire est égale à ∫ a b (g(x) - f(x)) dx.
Valeur moyenne d'une fonction
Soit f une fonction continue sur un intervalle [a ; b].
La valeur moyenne de f sur [a ; b] est égale à 1 b - a ∫ a b f(x) dx.