Baccalauréat Calcul de fonction dérivée
Dérivabilité d'une fonction sur un intervalle
Définition
Une fonction f définie sur un intervalle I est dérivable sur cet intervalle si elle est dérivable en tout point de cet intervalle.
La fonction dérivée d'une fonction f, notée f ', associe à chaque point a de l'intervalle I la dérivée de f en ce point f '(a).
Théorème
Les fonctions polynômes sont dérivables en tout nombre réel.
Les fonctions rationnelles sont dérivables en tout point de leurs domaines de définition.
Les fonctions définies par une expression comportant des racines carrées sont également dérivables en tout point de leurs domaines de définition.
Remarque
Rappelons du chapitre précédent que la dérivée d'une fonction f en un point a est calculé par :
lim x→a f(x) - f(a) x – a
En ce chapitre, nous verrons des règles permettant de calculer la fonction dérivée d'une fonction à partir de l'expression de celle-ci.
Fonctions dérivées de fonctions usuelles
| Fonction f(x) | Fonction dérivée f '(x) |
|---|---|
| k (constante) | 0 |
| xn | n xn-1 |
| 1 x | -1 x2 |
| 1 xn | -n xn+1 |
| √x | 1 2 √x |
Remarque
Il convient d'apprendre les 3 dernières règles à savoir :
( 1 x ) ' = -1 x2
( 1 xn ) ' = -n xn+1
(√x) ' = 1 2 √x
Pourtant, ces règles sont déductibles de la règle :
(xn) ' = n xn-1
Pour cela, il faut se rappeler que :
1 x = x-1
1 xn = x-n
√x = x1/2
Donc
( 1 x ) ' = (x-1) ' = -1 x-1-1 = -1 x2
( 1 xn ) ' = (x-n) ' = -n x-n-1 = -n xn+1
(√x) ' = (x½) ' = 1 2 x½-1 = 1 2 √x
Opérations sur les fonctions
| Fonction f(x) | Fonction dérivée f '(x) | Exemples |
|---|---|---|
| u(x) + v(x) | u '(x) + v '(x) | (x3 + x2 - 3) ' = 3x2 + 1 |
| k u(x) | k u '(x) | (3x2 + 2x) ' = 3(2x) + 2 = 6x + 2 |
| u(x) . v(x) | u '(x) . v(x) + u(x) . v '(x) | Exemples de produits |
| 1 v(x) | -v '(x) (v(x))2 | Exemples d'inverses |
| u(x) v(x) | u '(x) . v(x) - u(x) . v '(x) (v(x))2 | Exemples de quotients |
| v(u(x)) | u '(x) . v '(u(x)) | Exemples de composées |
| u -1(x) | 1 u '(u -1(x)) |
Exemples
Exemples de produits
Déterminer les fonctions dérivées des fonctions f,g et h définies par :
Solution
Bien entendu, nous pouvons d'abord développer les expressions de f(x),g(x) et h(x) avant de dériver. Vous pouvez vérifier que le résultat obtenu est le même.
Cas de la fonction h
Donc
Exemples d'inverses
Déterminer les fonctions dérivées des fonctions f,g et h définies par :
Solution
Exemples de quotients
Déterminer les fonctions dérivées des fonctions f,g et h définies par :
Solution
Exemples de composées
Nous appliquons la règle de dérivée de composée à des exemples de puissance et de racine.
Déterminer les fonctions dérivées des fonctions f,g et h définies par :
Solution
Théorème
Si une fonction f est dérivable sur un intervalle I, alors
- Si f '(x) > 0 pour tout x de I alors la fonction f est croissante sur I.
- Si f '(x) < 0 pour tout x de I alors la fonction f est décroissante sur I.
- Si f '(x) = 0 pour tout x de I alors la fonction f est constante sur I.
Théorème
Si une fonction f est dérivable sur un intervalle I et f ' s'annule en un point x0 de I avec changement de signe alors f(x0) est un extremum relatif pour la fonction f.
Exemple
Soit la fonction numérique f définie par :
f(x) = x3
La fonction dérivée de f :
f '(x) = 3x2
La fonction dérivée de f est toujours positive et s'annule en 0. Tableau de variation :
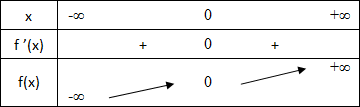
La fonction dérivée de f s'annule en 0, mais ne change pas de signe. La courbe représentative de f a une tangente horizontale en 0. Mais, f(0) n'est pas un extremum pour la fonction f.