Baccalauréat Exercices Dérivabilité en un point
Consulter le cours Dérivabilité en un point
Exercice 1
Etudier la dérivabilité aux points :
- -1 à droite
- 1
- 3 à gauche
et déterminer les équations des tangentes en ces points à la courbe représentative pour la fonction f définie par
Dérivabilité à droite du point -1
La fonction f n'est pas dérivable au point -1.
La tangente à la représentation graphique de la fonction f au point -1 a pour équation :
x = -1
Dérivabilité au point 1
La fonction f est dérivable au point 1.
La tangente à la représentation graphique de la fonction f au point 1 a pour équation :
y = f '(1) (x - 1) + f(1)
y = 2
Dérivabilité à gauche du point 3
La fonction f n'est pas dérivable au point 3.
La tangente à la représentation graphique de la fonction f au point 3 a pour équation :
x = 3
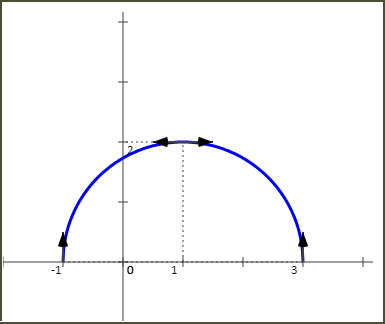
A titre indicatif la représentation graphique de la fonction f est comme suit :
Exercice 2
Etudier la dérivabilité aux points :
- -2 à droite
- -1
- 1
et déterminer les équations des tangentes en ces points à la courbe représentative pour la fonction f définie par
Dérivabilité à droite du point -2
La fonction f n'est pas dérivable au point -2.
La tangente à la représentation graphique de la fonction f au point -2 a pour équation :
x = -2
Dérivabilité au point -1
La fonction f est dérivable au point -1.
La tangente à la représentation graphique de la fonction f au point -1 a pour équation :
y = f '(-1) (x + 1) + f(-1)
y = 2
Dérivabilité au point 1
La fonction f est dérivable au point 1.
La tangente à la représentation graphique de la fonction f au point 1 a pour équation :
y = f '(1) (x - 1) + f(1)
y = -√3x + √3
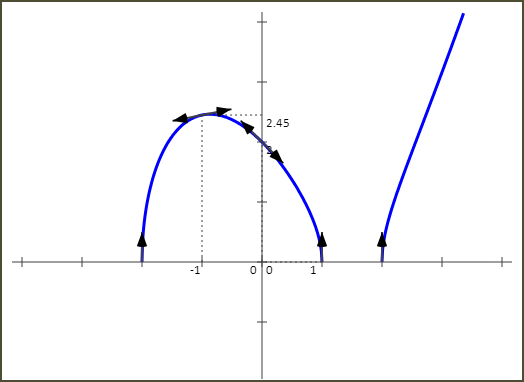
A titre indicatif la représentation graphique de la fonction f est comme suit :

Exercice 3
Etudier la dérivabilité aux points :
- -2 à droite
- -1
- 0
- 1 à gauche
et déterminer les équations des tangentes en ces points à la courbe représentative pour la fonction f définie par
Dérivabilité à droite du point -2
La fonction f n'est pas dérivable au point -2.
La tangente à la représentation graphique de la fonction f au point -2 a pour équation :
x = -2
Dérivabilité au point -1
La fonction f est dérivable au point -1.
La tangente à la représentation graphique de la fonction f au point -1 a pour équation :
Dérivabilité au point 0
La fonction f est dérivable au point 0.
La tangente à la représentation graphique de la fonction f au point 0 a pour équation :
y = f '(0) (x - 0) + f(0)
y = - x + 2
Dérivabilité à gauche du point 1
La fonction f n'est pas dérivable au point 1.
La tangente à la représentation graphique de la fonction f au point 1 a pour équation :
x = 1
A titre indicatif la représentation graphique de la fonction f est comme suit :