Baccalauréat Exercices Etude de fonctions
Consulter le cours Etude de fonctions
Exercice 1
Soit la fonction numérique f définie par :
f(x) = 1 3 x3 - x2 - 3x + 3
- Calculer les limites en -∞ et +∞ de f(x).
- Calculer f '(x).
- Etudier le signe de f '(x) et dresser son tableau de variations
- Calculer f "(x).
- Etudier le signe de f "(x). En déduire que le point I(1, -2 3 ) est un point d'inflexion pour la courbe représentative de la fonction Cf.
- Calculer f '(1). Déterminer l'équation de la tangente à Cf au point d'abscisse 1.
- Montrer que le point I(1, -2 3 ) est centre de symétrie pour la courbe représentative Cf.
- Tracer la courbe Cf.
Solution
1 - Limites en -∞ et +∞ de f(x)
lim
x→-∞
f(x) =
lim
x→-∞
1
3
x3 = -∞
lim
x→+∞
f(x) =
lim
x→+∞
1
3
x3 = +∞
2 - Calcul de f '(x)
f '(x) = x2 - 2x - 3
3 - Signe de f '(x) et tableau de variations
Pour trouver les zéros pour le polynôme "x2 - 2x - 3", on calcule le discriminant
Δ = 16.
On calcule les zéros pour le polynôme "x2 - 2x - 3"
x1 = -1
x2 = 3
Le tableau de variations est comme suit :
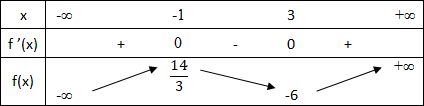
4 - Calcul de f "(x)
f "(x) = 2x - 2
5 - Signe de f "(x) et point d'inflexion
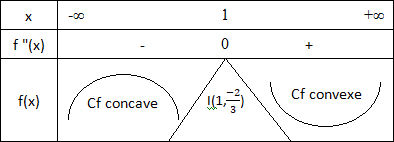
Le point I(1, -2 3 ) est un point d'inflexion pour la courbe Cf car f "(x) s'annule en 1 avec changement de signe.
6 - Calcul de f '(1)
f '(1) = -4
L'équation de la tangente à Cf au point d'abscisse 1
y = f '(1) (x - 1) + f(1) = -4x + 10 3
7 - Montrons que le point I(1, -2 3 ) est centre de symétrie pour la courbe représentative Cf.
8 - Courbe Cf
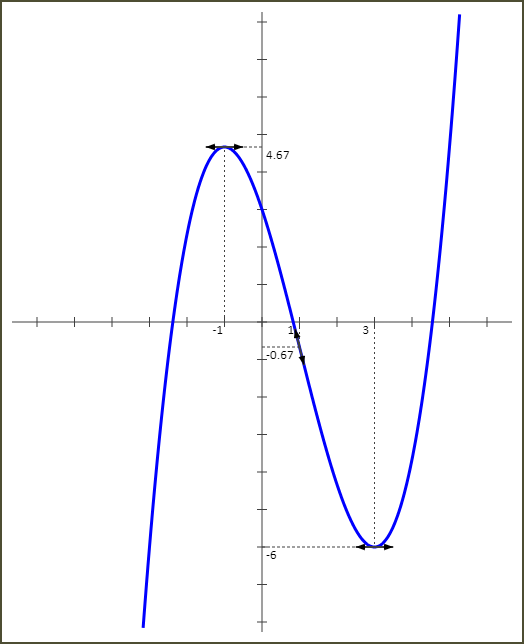
Exercice 2
Soit la fonction g définie par :
g(x) = 2x2 + x - 2 2x + 3
- Déterminer le domaine de définition Dg.
- Calculer les limites de g(x) aux bornes de Dg. En déduire que la courbe représentative de la fonction Dg admet une asymptote verticale.
- Calculer g '(x).
- Etudier le signe de g '(x) et dresser son tableau de variations
- Montrer que la droite d'équation y=x-1 est une asymptote pour la courbe représentative Cg.
- Tracer la courbe Cg.
Solution
1 - Domaine de définition de g
Il faut que 2x + 3 ≠ 0 donc x ≠ -3 2
Donc
Dg = ]-∞; -3 2 [∪] -3 2 ;+∞[
2 - Limites aux bornes de Dg
La courbe Dg admet donc une asymptote verticale d'équation x= -3 2 .
3 - Calcul de g '(x)
4 - Signe de g '(x) et tableau de variations
Pour trouver les zéros pour le polynôme "4x2 + 12x + 7", on calcule le discriminant
Δ = 144-4.4.7 = 32.
On calcule les zéros pour le polynôme "4x2 + 12x + 7"
x1 =
-3 - √2
2
x2 =
-3 + √2
2
Le tableau de variations est comme suit :
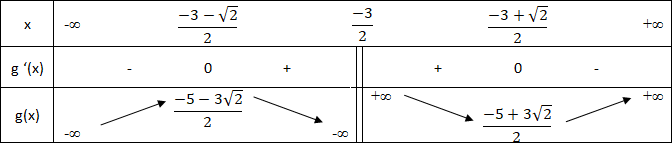
5 - Montrons que la droite d'équation y=x-1 est une asymptote pour la courbe représentative Cg
Pour cela, calculons d'abord g(x)-y.
6 - Courbe Cg
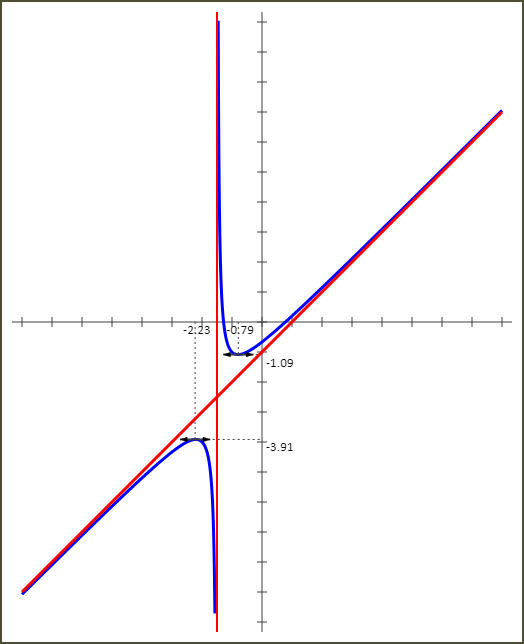
Exercice 3
Soit la fonction numérique f définie par :
f(x) = x √x2 + 1
- Calculer les limites en -∞ et +∞ de f(x).
- Calculer f '(x).
- Etudier le signe de f '(x) et dresser son tableau de variations
- Calculer f "(x).
- Etudier le signe de f "(x). En déduire que le point I(0,0) est un point d'inflexion pour la courbe représentative de la fonction Cf.
- Calculer f '(0). Déterminer l'équation de la tangente à Cf au point d'abscisse 0.
- Montrer que le point I(0,0) est centre de symétrie pour la courbe représentative Cf.
- Calculer les limites en -∞ et +∞ de f(x) x . Déduire.
- Tracer la courbe Cf.
Solution
1 - Limites en -∞ et +∞ de f(x)
lim
x→-∞
f(x) = -∞
lim
x→+∞
f(x) = +∞
2 - Calcul de f '(x)
3 - Signe de f '(x) et tableau de variations
f '(x) est toujours positive. Le tableau de variations est comme suit :
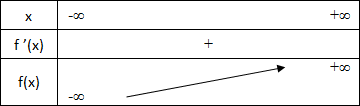
4 - Calcul de f "(x)
5 - Signe de f "(x) et point d'inflexion
f "(x) s'annule au point 0 avec changement de signe. Le point I(0,0) est un point d'inflexion pour la courbe Cf.
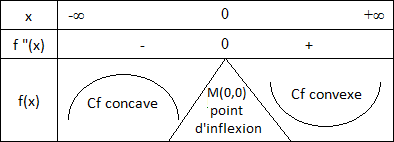
6 - Calcul de f '(0)
f '(0) = 1
L'équation de la tangente à Cf au point d'abscisse 0
y = f '(0) (x - 0) + f(0) = x
7 - Montrons que le point I(0,0) est centre de symétrie pour la courbe représentative Cf.
8 - Branches infinies
lim
x→-∞
f(x)
x
=
lim
x→-∞
√x2 + 1 = +∞
lim
x→+∞
f(x)
x
=
lim
x→+∞
√x2 + 1 = +∞
La courbe Cf a une branche parabolique de direction asymptotique l'axe des ordonnées au voisinage de -∞ et +∞.
9 - Courbe Cf