Baccalauréat Etude de fonctions
Elèments de l'étude de fonctions
L'étude de fonctions se déroule selon les étapes suivantes
2 - Calcul de la fonction dérivée et l'étude de signe de cette fonction
4 - Étude des branches infinies
5 - Étude de concavité de la courbe représentative de la fonction
6 - Étude de position relative de la courbe représentative de la fonction
7 - Centre de symétrie ou axe de symétrie de la courbe représentative de la fonction
8 - Établissement de la courbe représentative de la fonction
1 - Domaine de définition et limites aux bornes
Prenons à titre d'exemple la fonction numérique f définie par :
f(x) = -1 x + 2 - 2x + 3
La fonction f est définie lorsque x+2≠0. Donc x≠-2.
Le domaine de définition de la fonction f est donc :
Df = ]-∞;-2[ ∪ ]-2;+∞[
Il faut ensuite déterminer les limites aux bornes du domaine de définition. C'est à dire pour notre cas, les limites en -∞, à gauche de -2, à droite de -2 et en +∞ :
lim
x→-∞
f(x) =
lim
x→-∞
(
-1
x + 2
- 2x + 3) = +∞
lim
x→-2
x < -2
f(x) =
lim
x→-2
x < -2
(
-1
x + 2
- 2x + 3) = +∞
lim
x→-2
x > -2
f(x) =
lim
x→-2
x > -2
(
-1
x + 2
- 2x + 3) = -∞
lim
x→+∞
f(x) =
lim
x→+∞
(
-1
x + 2
- 2x + 3) = -∞
2 - Calcul de la fonction dérivée et détermination de son signe
Continuons avec l'exemple de la fonction numérique f définie par :
f(x) = -1 x + 2 - 2x + 3
Calculons la fonction dérivée :
Pour trouver les zéros pour le polynôme "2x2 + 8x + 7", on calcule le discriminant
Δ = 8.
On calcule les zéros pour le polynôme "2x2 + 8x + 7"
x1 =
-4 - √2
2
x2 =
-4 + √2
2
Donc
f '(x) > 0 pour x ∈ ]
-4 - √2
2
;
-4 + √2
2
[
f '(x) < 0 pour x ∈ ]-∞;
-4 - √2
2
[ ∪ ]
-4 + √2
2
;+∞[
Donc
f est croissante pour x ∈ ]
-4 - √2
2
;
-4 + √2
2
[
f est décroissante pour x ∈ ]-∞;
-4 - √2
2
[ ∪ ]
-4 + √2
2
;+∞[
Autre Exemple:
Soit la fonction g définie par :
g(x) = x3 8 - 3x 2 + 1
Calculons la fonction dérivée :
g '(x) = 3x2 8 - 3 2 = 3 8 (x2 - 4)
Donc g ' s'annule en :
x1 = -2
x2 = 2
Donc
f '(x) < 0 pour x ∈ ]-2;2[
f '(x) > 0 pour x ∈ ]-∞;-2[ ∪ ]2;+∞[
Donc
f est décroissante pour x ∈ ]-2;2[
f est croissante pour x ∈ ]-∞;-2[ ∪ ]2;+∞[
Consulter le lien Etude de signe de fonction pour les techniques de détermination des signes de fonctions.
3 - Tableau de variation
Le tableau de variation d'une fonction est un tableau qui montre le sens de variation de la fonction en se basant sur le signe de la fonction dérivée.
Le tableau de variation met en évidence les bornes du domaine de définition ainsi que les points où la fonction dérivée s'annule. Il faut donc calculer les limites ou bien les images de ces points.
Continuons avec l'exemple de la fonction numérique f définie par :
f(x) = -1 x + 2 - 2x + 3
Le tableau de variation est comme suit :

4 - Etude des branches infinies
Le tableau suivant montre les cas où la courbe représentative (C) d'une fonction numérique f a une asymptote ou une branche parabolique.
Un droite est une asymptote pour la courbe (C), si celle-ci tend à s'approcher de plus en plus de cette droite sans jamais la couper (Voir les exemples dans le tableau suivant).
La courbe (C) a une branche parabolique de direction une droite au voisinage de l'infini, si elle apparait pratiquement parallèle à cette droite. En effet la courbe s'éloigne mais doucement de cette droite.
| Limites à vérifier | Résultat | Exemple | Courbe | ||
|---|---|---|---|---|---|
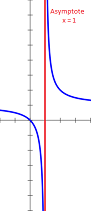
| lim x→a f(x) = ±∞ | La courbe (C) a une asymptote verticale d'équation x = a | f(x) =
1
x - 1
+ 1 lim x→1 x < 1 f(x) = -∞ lim x→1 x > 1 f(x) = +∞ |
 |
||
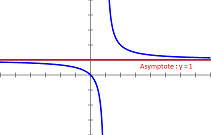
| lim x→±∞ f(x) = a | La courbe (C) a une asymptote horizontale d'équation y = a au voisinage de l'infini | f(x) =
1
x - 1
+ 1 lim x→-∞ f(x) = 1 lim x→+∞ f(x) = 1 |
 |
||
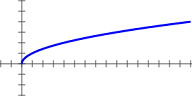
| lim x→±∞ f(x) = ±∞ | lim x→±∞ f(x) x = 0 | La courbe (C) a une branche parabolique de direction asymptotique l'axe des abscisses au voisinage de l'infini | f(x) = √x lim x→+∞ f(x) x = 0 |
 |
|
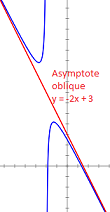
| lim x→±∞ f(x) x = a (≠0) | lim x→±∞ (f(x) - ax) = b | La courbe (C) a une asymptote oblique d'équation y = ax + b au voisinage de l'infini | f(x) =
-1
x + 2
- 2x + 3 lim x→±∞ f(x) x = -2 lim x→±∞ f(x) + 2x = 3 |
 |
|
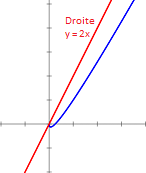
| lim x→±∞ (f(x) - ax) = ±∞ | La courbe (C) a une branche parabolique de direction asymptotique la droite d'équation y = ax au voisinage de l'infini | f(x) = 2x - √x lim x→+∞ f(x) x = 2 lim x→+∞ f(x) - 2x = -∞ |
 |
||
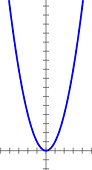
| lim x→±∞ f(x) x = ±∞ | La courbe (C) a une branche parabolique de direction asymptotique l'axe des ordonnées au voisinage de l'infini | f(x) = x2 lim x→-∞ f(x) x = -∞ lim x→+∞ f(x) x = +∞ |
 |
||
Il ressort du tableau que si la limite en l'infini de f(x) est égale à l'infini, alors il faut calculer la limite de f(x) x . Et si le résultat de cette limite est un nombre "a" différent de 0, alors il faut calculer la limite de f(x)-ax.
C'est le cas pour la fonction f définie par :
f(x) = -1 x + 2 - 2x + 3
Calculons les limites
lim
x→-∞
f(x) = +∞
lim
x→-∞
f(x)
x
= -2
lim
x→-∞
(f(x) + 2x) = 3
On en déduit que la droite d'équation y=-2x+3 est une asymptote oblique pour la courbe représentative de la fonction f au voisinage de -∞. Vérifier de la même manière que c'est le cas également au voisinage de +∞.
N.B. Concernant l'asymptote oblique, vous pouvez avoir la question de manière différente.
Soit, montrer que la droite d'équation y=-2x+3 est une asymptote oblique pour la courbe représentative de la fonction f au voisinage de ±∞.
Ou bien, Calculer la limite en ±∞ de f(x)-(-2x+3). En déduire...
Dans ces deux cas, il faut calculer la limite de f(x)-(-2x+3) et si vous obtenez 0, alors vous pouvez déduire que la droite d'équation y=-2x+3 est une asymptote oblique pour la courbe représentative de la fonction f au voisinage de ±∞.
5 - Etude de concavité de la courbe représentative de la fonction
La courbe représentative d'une fonction numérique est dite convexe si la tangente à un point quelconque de cette courbe est située au-dessous de la courbe.
La courbe représentative d'une fonction numérique est dite cancave si la tangente à un point quelconque de cette courbe est située au-dessus de la courbe.
Un point d'inflexion est un point où la courbe change de concavité.
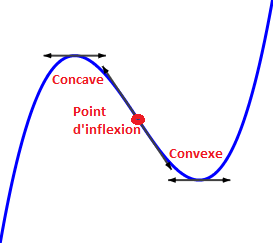
Pour étudier la concavité, il faut calculer la dérivée seconde de la fonction. Il s'agit de la fonction dérivée de la fonction dérivée de la fonction. Elle est notée f ".
Il faut ensuite déterminer le signe de f "(x).
- Si f "(x) > 0 pour tout x d'un intervalle I alors la courbe de la fonction f est convexe sur I.
- Si f "(x) < 0 pour tout x d'un intervalle I alors la courbe de la fonction f est concave sur I.
- Si f "(x0) = 0 avec changement de signe alors la courbe de la fonction f a un point d'inflexion en x0.
Exemple
Soit la fonction g définie par :
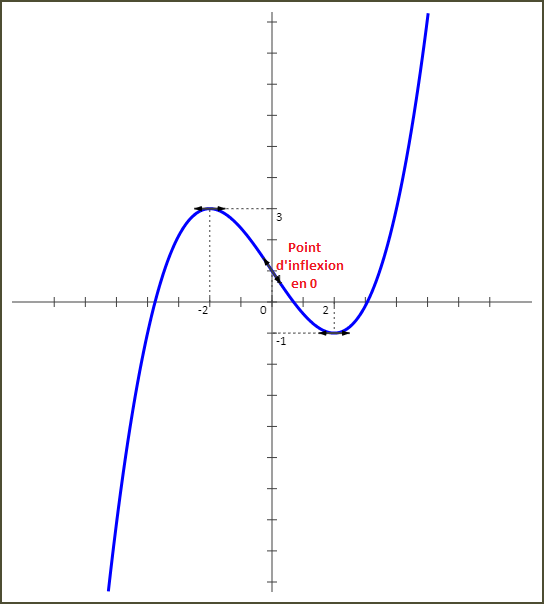
g(x) = x3 8 - 3x 2 + 1
Calculons la fonction dérivée :
g '(x) = 3x2 8 - 3 2
Calculons la fonction dérivée seconde :
g "(x) = 3x 4
Donc :
- g "(x) > 0 pour tout x > 0 donc la courbe de la fonction g est convexe sur ]0;+∞[.
- g "(x) < 0 pour tout x < 0 donc la courbe de la fonction g est concave sur ]-∞;0[.
- g "(0) = 0 avec changement de signe donc la courbe de la fonction g a un point d'inflexion en 0.
6 - Etude de positions relatives de la courbe représentative de la fonction
La position relative de la courbe d'une fonction f par rapport à une droite d'équation y=ax+b est déterminée par le calcul de :
f(x) - y
Il faut ensuite déterminer le signe de cette expression.
- Si f(x) - y > 0 pour tout x d'un intervalle I alors la courbe de la fonction f est au dessus de la droite sur I.
- Si f(x) - y < 0 pour tout x d'un intervalle I alors la courbe de la fonction f est au dessous de la droite sur I.
On peut utiliser cela pour déterminer la position relative de la courbe par rapport à une asymptote ou bien par rapport à une tangente.
On peut également étudier la position relative de la courbe d'une fonction f par rapport à celle d'une autre fonction g :
- Si f(x) - g(x) > 0 pour tout x d'un intervalle I alors la courbe de la fonction f est au dessus de celle de g sur I.
- Si f(x) - g(x) < 0 pour tout x d'un intervalle I alors la courbe de la fonction f est au dessous de celle de g sur I.
7 - Centre de symétrie ou axe de symétrie de la courbe représentative de la fonction
Théorème
La droite d'équation y=a est un axe de symétrie pour la courbe représentative d'une fonction f, si pour tout nombre x de Df, (2a - x) appartient à Df et
f(2a - x) = f(x)
Théorème
Le point M(a,b) est un centre de symétrie pour la courbe représentative d'une fonction f, si pour tout nombre x de Df, (2a - x) appartient à Df et
f(2a - x) = 2b - f(x)
Exemple Axe de symétrie:
Soit la fonction f définie par :
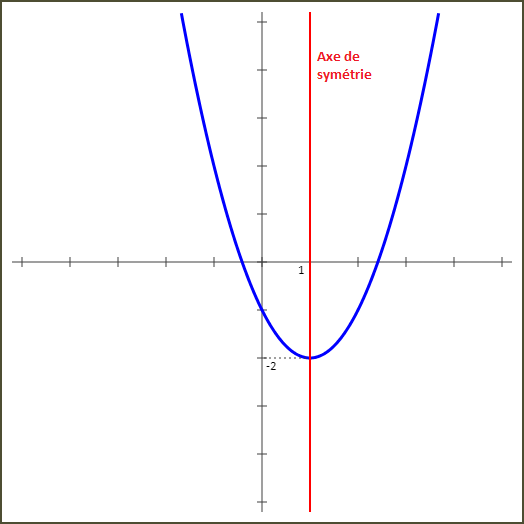
f(x) = x2 - 2x - 1
Vérifions que la droite d'équation y=1 est un axe de symétrie pour la courbe de la fonction f :
A titre indicatif, voici la courbe de la fonction
Exemple Centre de symétrie:
Soit la fonction g définie par :
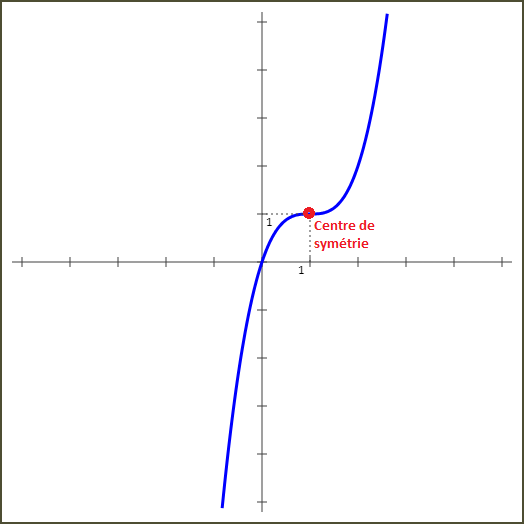
g(x) = x3 - 3x2 + 3x
Vérifions que le point M(1,1) est un centre de symétrie pour la courbe de la fonction g :
A titre indicatif, voici la courbe de la fonction
8 - Etablissement de la courbe représentative de la fonction
Pour dresser la courbe représentative d'une fonction, il faut :
- Utiliser le tableau de variation pour dessiner les tangentes horizontales, c'est à dire aux points où la fonction dérivée s'annule.
- Utiliser l'étude de concavité pour relever les points d'inflexion. Dessiner les tangentes à la courbe en ces points.
- Dessiner également les branches infinies.
Ces éléments seront utilisés comme repères pour le dessin de la courbe.
Cas de la fonction :
f(x) = -1 x + 2 - 2x + 3
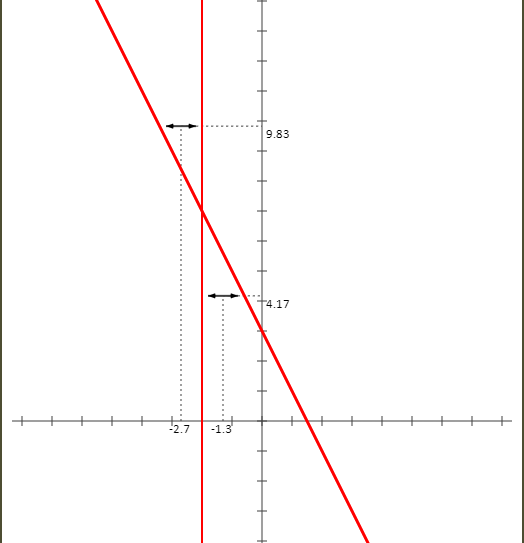
Cas de la fonction :
g(x) = x3 8 - 3x 2 + 1
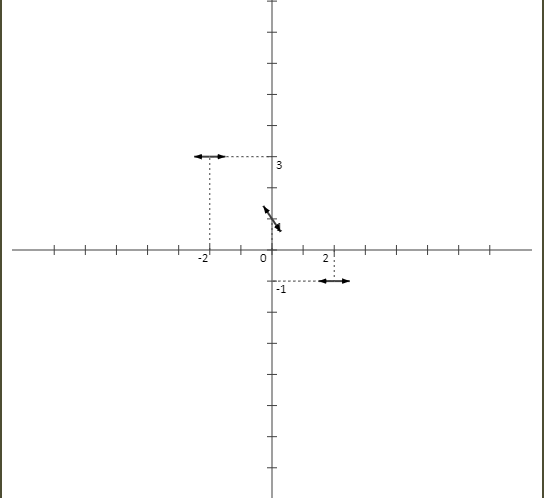
Tracer ensuite la courbe en tenant compte de ces repères, du tableau de variation et des autres études mentionnées dans cette page.
Cas de la fonction :
f(x) = -1 x + 2 - 2x + 3
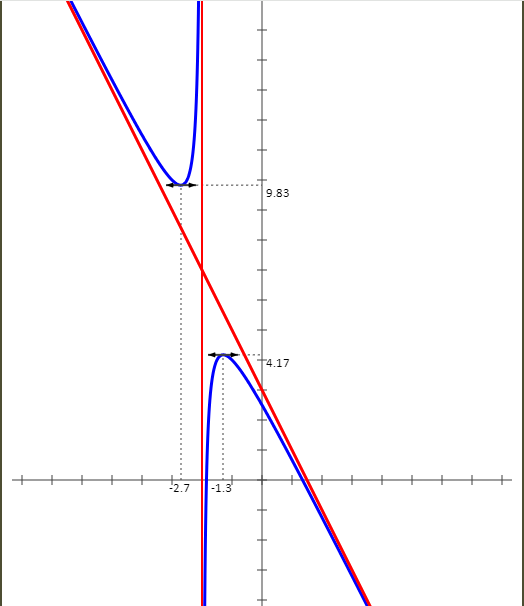
Cas de la fonction :
g(x) = x3 8 - 3x 2 + 1