Baccalauréat Exercices Exponentielle de base a

Consulter le cours Exponentielle de base a

Exercice 1

Résoudre dans ℝ les équations suivantes

  1. 10x - 2 = 103
  2. 10x - 5 - 103x + 1 = 0
  3. 104x - 1 = 1 000

Solution

1 - L'équation

L'ensemble de solutions de l'équation est S = {5}

2 - L'équation

L'ensemble de solutions de l'équation est S = {-3}

3 - L'équation

L'ensemble de solutions de l'équation est S = {1}

Exercice 2

Résoudre dans ℝ les inéquations suivantes

  1. 102x - 3 / 10x + 1 > 10
  2. 103x - 2 / 10x + 1 > 102x - 3 / 10x + 4
  3. 10x+1 + 10x-1 < 101

Solution

1 - L'inéquation

L'ensemble de solutions de l'inéquation est S = ] 5 ; +∞ [

2 - L'inéquation

L'ensemble de solutions de l'inéquation est S = ] -4 ; +∞ [

3 - L'inéquation

L'ensemble de solutions de l'inéquation est S = ] -∞ ; 1 [

Exercice 3

Etude de la fonction f définie sur ℝ* par :

f(x) = 10x / x

  1. Calculer les limites en -∞, 0 et +∞ de f(x). Déduire
  2. Calculer f '(x).
  3. Etudier le signe de f '(x) et dresser son tableau de variations
  4. Calculer f "(x).
  5. Etudier le signe de f "(x). Etudier la concavité de la courbe représentative de la fonction Cf.
  6. Calculer la limite en +∞ de f(x) / x . Déduire
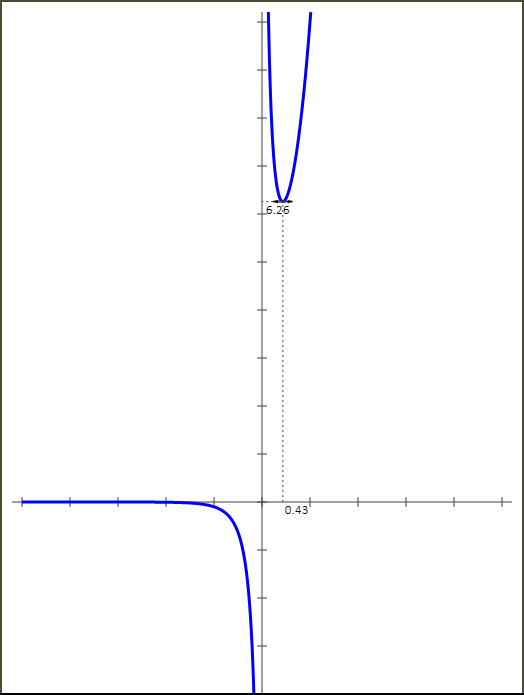
  7. Tracer la courbe Cf.

Solution

1 - Limites en -∞, 0 et +∞ de f(x)

lim x→-∞ f(x) = lim x→-∞ 10x / x = 0

lim x→0 x < 0 f(x) = lim x→0 x < 0 10x / x = -∞

lim x→0 x > 0 f(x) = lim x→0 x > 0 10x / x = +∞

lim x→+∞ f(x) = lim x→+∞ 10x / x = +∞

2 - Calcul de f '(x)

3 - Signe de f '(x) et tableau de variations

f '(x) > 0 ⇒ ln(10) . x - 1 > 0 ⇒ x > 1 / ln(10)

Calcul de f( 1 / ln(10) ).

f( 1 / ln(10) ) = ln(10) . 101/ln(10) = ln(10) . eln(10).1/ln(10) = e ln(10)

Le tableau de variations est comme suit :

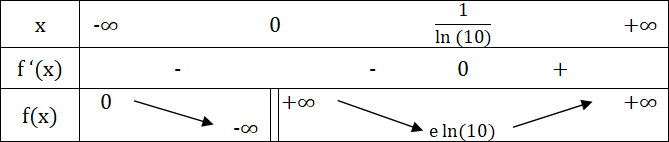
Etude Fonction Exponentielle de base a

4 - Calcul de f "(x)

5 - Signe de f "(x) et concavité de la courbe Cf

Etudions le signe du polynôme de second degré

(ln(10))2 x2 - 2 ln(10) x + 2

Le discriminant

Δ = 4 (ln(10))2 - 4 . 2 . (ln(10))2 = -4 (ln(10))2

Le discriminant est toujours négatif. le polynôme est toujours positif.

Le tableau de concavité pour la courbe Cf est comme suit :

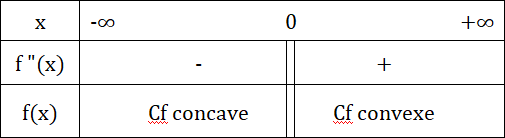
Etude Fonction Exponentielle de base a

6 - Branches infinies

lim x→+∞ f(x) / x = lim x→+∞ 10x / x2 = +∞

La courbe Cf a une branche parabolique de direction asymptotique l'axe des ordonnées au voisinage de +∞.

7 - Courbe Cf

Etude Fonction Exponentielle de base a