Baccalauréat Exponentielle de base a
Définition
Une fonction exponentielle de base a (a ∈ ℝ+-{1}), notée expa, est définie sur ℝ par
expa(x) = ax = ex ln(a)
La fonction exponentielle néperienne est la fonction exponentielle de base e, car ln(e) = 1.
Exemple
Il est utilisé principalement l'exponentielle de base 10 qui est la fonction puissance de 10. C'est à dire de la fonction définie par 10x.
101 = 10
103 = 1 000
10-2 = 0,01
Propriétés
On retrouve les mêmes propriétés connues pour les puissances :
expa(0) = a0 = 1
expa(1) = a1 = a
La fonction exponentielle de base a est
- strictement croissante sur l'ensemble ℝ si a > 1.
- strictement décroissante sur l'ensemble ℝ si a < 1.
Donc
x = y ⇔ ax = ay
Si a > 1 alors 0 < x < y ⇔ ax < ay
Si a < 1 alors 0 < x < y ⇔ ax > ay
Et
x = 1 ⇔ ax = 0
Si a > 1 alors 0 < x < 1 ⇔ ax < 0 et x > 1 ⇔ ax > 0
Si a < 1 alors 0 < x < 1 ⇔ ax > 0 et x > 1 ⇔ ax < 0
Autre propriétés
ax+y = ax . ay
a-x =
1
ax
ax-y =
ax
ay
(ax)y = ax y
(a . b)x = ax . bx
Exemples
Calculer
1 000 1003 . (0,01)4
Résoudre l'équation
ex + 1 = e4 - x
L'ensemble de solutions de l'équation est S = { 3 2 }
Limites usuelles
Limites en -∞
Si a > 1
lim x→-∞ ax = 0
lim x→-∞ xn ax = 0 (n ∈ ℕ*)
Si 0 < a < 1
lim x→-∞ ax = +∞
lim
x→-∞
ax
xn
= -∞ (Si n ∈ ℕ* est impaire)
et
lim
x→-∞
ax
xn
= +∞ (Si n ∈ ℕ* est paire)
Limites en +∞
Si a > 1
lim x→+∞ ax = +∞
lim x→+∞ ax xn = +∞ (n ∈ ℕ*)
Si 0 < a < 1
lim x→+∞ ax = 0
lim x→+∞ xn ax = 0 (n ∈ ℕ*)
Limites en 0
lim x→0 ax - 1 x = ln(a)
NB. Cette limite n'est autre que la dérivée de la fonction exponentielle de base a en 0.
Dérivée de la fonction exponentielle de base a
La fonction dérivée de la fonction exponentielle de base a est la fonction définie sur ℝ par
f(x) = ln(a) ax
(au(x)) ' = u '(x) ln(a) au(x)
Exemple
Calculons la dérivée de la fonction f définie par
f(x) = 10x2 + 2x + 2
f '(x) = (x2 + 2x + 2) ' ln(10) 10x2 + 2x + 2 = (2x + 2) ln(10) 10x2 + 2x + 2
Branches infinies
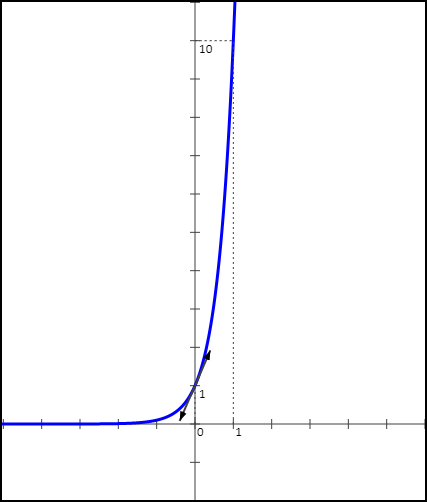
Si a > 1
Nous avons vu la limite au voisinage de -∞
lim x→-∞ ax = 0
La courbe représentative de la fonction exponentielle de base a admet une asymptote horizontale d'équation y = 0 (Axe des abscisses).
Concernant les limites au voisinage de +∞
lim x→+∞ ax = +∞
lim x→+∞ ax x = +∞
La courbe représentative de la fonction exponentielle de base a admet une branche parabolique de direction asymptotique l'axe des ordonnées au voisinage de +∞.
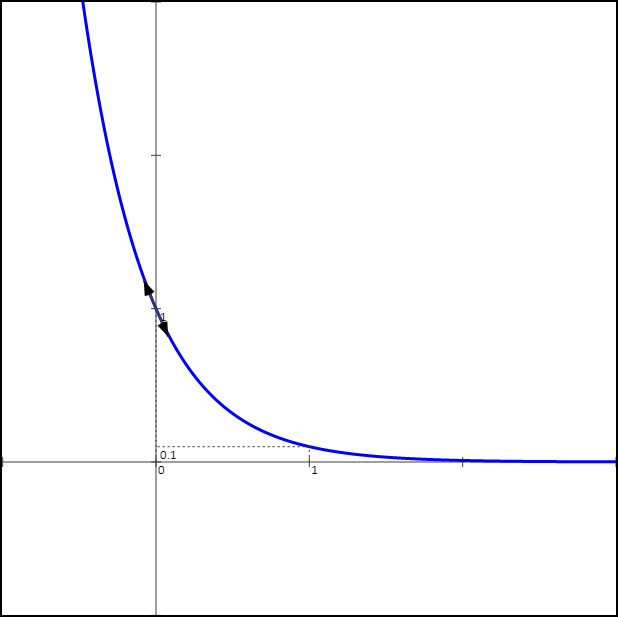
Si 0 < a < 1
Nous avons vu la limite au voisinage de +∞
lim x→+∞ ax = 0
La courbe représentative de la fonction exponentielle de base a admet une asymptote horizontale d'équation y = 0 (Axe des abscisses).
Concernant les limites au voisinage de -∞
lim x→-∞ ax = +∞
lim x→-∞ ax x = -∞
La courbe représentative de la fonction exponentielle de base a admet une branche parabolique de direction asymptotique l'axe des ordonnées au voisinage de -∞.
Tableau de variation
Si a > 1, le tableau de variation de la fonction exponentielle de base a est comme suit :
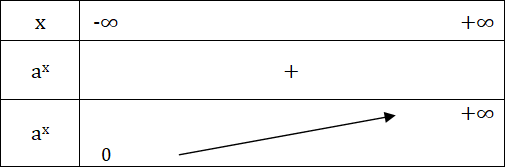
Si a < 1, le tableau de variation de la fonction exponentielle de base a est comme suit :

Courbe représentative de la fonction exponentielle de base a
Si a > 1, la courbe représentative de la fonction exponentielle de base a est de la forme (représenté l'exponentielle de base 10) :
Si a < 1, la courbe représentative de la fonction exponentielle de base a est de la forme (représenté l'exponentielle de base 0.1) :