Baccalauréat Exercices Logarithme de base a

Consulter le cours Logarithme de base a

Exercice 1

Résoudre dans ℝ les équations suivantes

  1. log(x - 2) = log(3)
  2. log(x - 5) - log(3x + 1) = 0
  3. log(3x - 1) = 3

Solution

1 - L'équation

log(x - 2) = log(3)

L'équation est définie si

x - 2 > 0 ⇒ x > 2

L'équation est définie sur ]2;+∞[

Or

5 ∈ ]2;+∞[

L'ensemble de solutions de l'équation est S = {5}

2 - L'équation

log(x - 5) - log(3x + 1) = 0

L'équation est définie si

x - 5 > 0 ⇒ x > 5
et
3x + 1 > 0 ⇒ x > -1 / 3

L'équation est définie sur ]5;+∞[

Or

-3 ∈ ]5;+∞[

L'ensemble de solutions de l'équation est S = {-3}

3 - L'équation

log(3x - 1) = 3

L'équation est définie si

3x - 1 > 0 ⇒ x > 1 / 3

L'équation est définie sur ] 1 / 3 ;+∞[

Or

333 ∈ ] 1 / 3 ;+∞[

L'ensemble de solutions de l'équation est S = {333}

Exercice 2

Résoudre dans ℝ les inéquations suivantes

  1. log(x - 3) - log(x + 1) > 1
  2. log(3x - 2) - log(x + 1) > log(2x - 3) - log(x + 4)
  3. log(x - 2) + log(2x - 1) < log(x2 - 3x + 2)

Solution

1 - L'inéquation

log(x - 3) - log(x + 1) > 1

L'inéquation est définie si

x - 3 > 0 ⇒ x > 3
et
x + 1 > 0 ⇒ x > -1

L'inéquation est définie sur ]3;+∞[

L'ensemble de solutions de l'inéquation est S = ]3;+∞[∩] -13 / 9 ;+∞[ = ]3;+∞[

2 - L'inéquation

log(3x - 2) - log(x + 1) > log(2x - 3) - log(x + 4)

L'inéquation est définie si

3x - 2 > 0 ⇒ x > 2 / 3
et
x + 1 > 0 ⇒ x > -1
et
2x - 3 > 0 ⇒ x > 3 / 2
et
x + 4 > 0 ⇒ x > -4

L'inéquation est définie sur ] 3 / 2 ;+∞[

Nous avons une inéquation de second degré. Le discriminant

Δ = 141

Les zéros pour le polynôme sont

x1 = -11 - √141 / 2 ≃ -11,44
x2 = -11 + √141 / 2 ≃ 0,44

Le polynôme est positif si

x ∈ ]-∞; -11 - √141 / 2 [U] -11 + √141 / 2 ;+∞[

L'ensemble de solutions de l'inéquation est S = ] 3 / 2 ;+∞[∩(]-∞; -11 - √141 / 2 [U] -11 + √141 / 2 ;+∞[) = ] 3 / 2 ;+∞[

3 - L'inéquation

log(x - 2) + log(2x - 1) < log(x2 - 3x + 2)

Remarquons que

x2 - 3x + 2 = (x - 1)(x - 2)

L'inéquation est définie si

x - 2 > 0 ⇒ x > 2
et
2x - 1 > 0 ⇒ x > 1 / 2
et
(x - 1)(x - 2) > 0 ⇒ x < 1 ou x > 2

L'inéquation est définie sur ]2;+∞[

L'ensemble de solutions de l'inéquation est S = ]2;+∞[∩]-∞;0[ = ∅

Exercice 3

Etude de la fonction f définie sur ]0;+∞[ par :

f(x) = x - log(x)

  1. Calculer les limites en 0 et +∞ de f(x).
  2. Calculer f '(x).
  3. Etudier le signe de f '(x) et dresser son tableau de variations
  4. Calculer f "(x).
  5. Etudier le signe de f "(x). En déduire que la courbe représentative de la fonction Cf est convexe sur l'ensemble de définition de f.
  6. Calculer la limite en +∞ de f(x) / x . et de f(x) - x. Déduire.
  7. Tracer la courbe Cf.

Solution

1 - Limites en 0 et +∞ de f(x)

lim x→0 x > 0 f(x) = lim x→0 x > 0 (x - log(x)) = +∞

lim x→+∞ f(x) = lim x→+∞ (x - log(x)) = lim x→+∞ (x(1 - log(x) / x )) = +∞

2 - Calcul de f '(x)

f '(x) = 1 - 1 / ln(10) . x

3 - Signe de f '(x) et tableau de variations

f '(x) > 0 ⇒ 1 - 1 / ln(10) . x > 0 ⇒ 1 > 1 / ln(10) . x ⇒ x > 1 / ln(10)

Calcul de f( 1 / ln(10) ).

f( 1 / ln(10) ) = 1 / ln(10) - log( 1 / ln(10) ) = 1 / ln(10) + log(ln(10)) = 1 + ln(ln(10)) / ln(10)

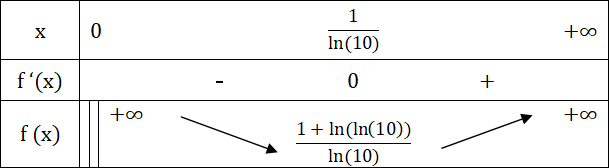
Le tableau de variations est comme suit :

Etude Fonction Logarithme de base a

4 - Calcul de f "(x)

f "(x) = 1 / ln(10) . x2

5 - Signe de f "(x) et concavité de la courbe Cf

ln(10) > 0 car (10 > 1) ⇒ f "(x) > 2

f "(x) est toujours positive. Donc la courbe Cf est convexe sur le domaine de définition de f.

6 - Branches infinies

lim x→+∞ f(x) / x = lim x→+∞ 1 + log(x) / x = 1

lim x→+∞ (f(x) - x) = lim x→+∞ (- log(x)) = -∞

La courbe Cf a une branche parabolique de direction asymptotique la droite d'équation y = x au voisinage de +∞.

7 - Courbe Cf

Etude Fonction Logarithme de base a