Baccalauréat Exercices Etude Fonction Logarithme
Consulter le cours Etude Fonction Logarithme népérien
Exercice 1
Etude de la fonction f définie sur ]0;+∞[ par :
f(x) = ln(x) + 1 x
- Calculer les limites en 0 et +∞ de f(x).
- Calculer f '(x).
- Etudier le signe de f '(x) et dresser son tableau de variations
- Calculer f "(x).
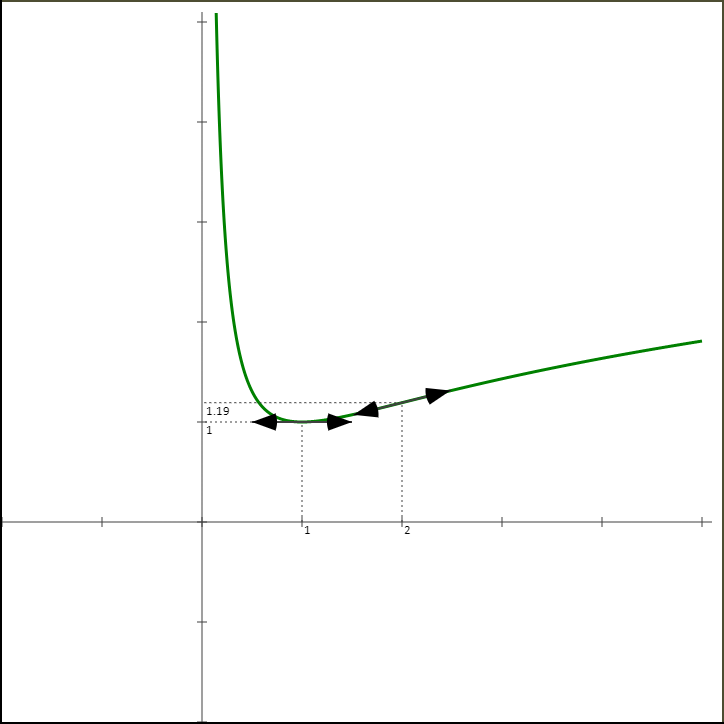
- Etudier le signe de f "(x). En déduire que le point I(2,ln(2+ 1 2 )) est un point d'inflexion pour la courbe représentative de la fonction Cf.
- Calculer f '(2). Déterminer l'équation de la tangente à Cf au point d'abscisse 0.
- Calculer la limite en +∞ de f(x) x . Déduire.
- Tracer la courbe Cf.
Solution
1 - Limites en 0 et +∞ de f(x)
lim x→0 x > 0 f(x) = lim x→0 x > 0 (ln(x) + 1 x ) = lim x→0 x > 0 ( 1 x (xln(x) + 1)) = +∞
lim x→+∞ f(x) = lim x→+∞ (ln(x) + 1 x ) = +∞
2 - Calcul de f '(x)
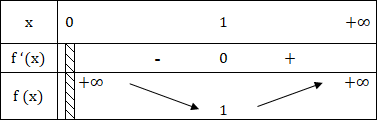
3 - Signe de f '(x) et tableau de variations
f '(x) > 0 ⇒ x - 1 > 0 ⇒ x > 1
Le tableau de variations est comme suit :
4 - Calcul de f "(x)
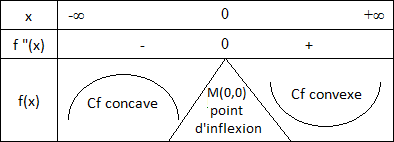
5 - Signe de f "(x) et point d'inflexion
f "(x) > 0 ⇒ x - 2 > 0 ⇒ x > 2
f "(x) s'annule au point 2 avec changement de signe. Le point I(2,ln(2+ 1 2 ) est un point d'inflexion pour la courbe Cf.
6 - Calcul de f '(2)
f '(2) = 1 4
L'équation de la tangente à Cf au point d'abscisse 2
y = f '(2) (x - 2) + f(2) = 1 4 x + ln(2)
7 - Branches infinies
lim
x→+∞
f(x)
x
=
lim
x→+∞
ln(x)
x
+
1
x2
= 0
La courbe Cf a une branche parabolique de direction asymptotique l'axe des ordonnées au voisinage de +∞.
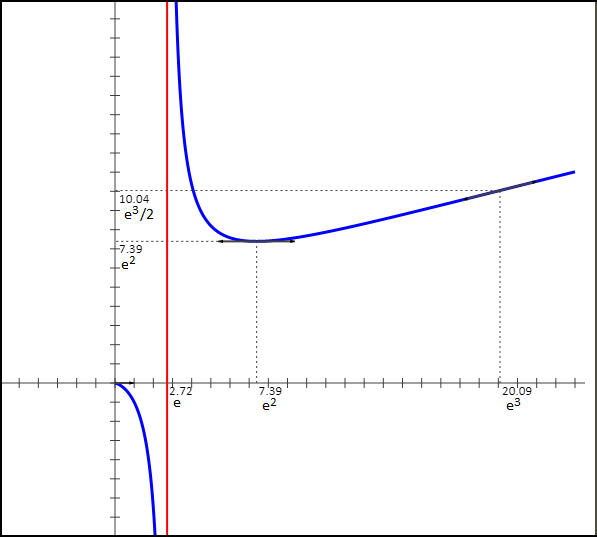
8 - Courbe Cf
Exercice 2
Etude de la fonction f définie sur [0;e[U]e;+∞[ par :
f(x) =
x
ln(x) - 1
pour x ≠ 0
f(0) = 0
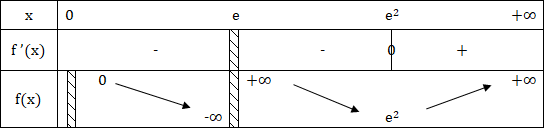
- Calculer la limite en 0 de f(x). Déduire.
- Calculer la limite en e de f(x). Déduire.
- Calculer la limite en +∞ de f(x). Calculer la limite en +∞ de f(x) x . Déduire.
- Etudier la dérivabilité de f à droite de 0. Déduire la tangente en 0 à la courbe représentative de la fonction Cf.
- Calculer f '(x).
- Etudier le signe de f '(x) et dresser son tableau de variations
- Calculer f "(x).
- Etudier le signe de f "(x). En déduire que le point I(e3, e3 2 ) est un point d'inflexion pour la courbe représentative de la fonction Cf.
- Calculer f '(2). Déterminer l'équation de la tangente à Cf au point d'abscisse 2.
- Tracer la courbe Cf.
Solution
1 - Limite en 0
lim x→0 x > 0 f(x) = lim x→0 x > 0 x ln(x) - 1 = 0
La limite en 0 à droite de f(x) est égale à f(0). Donc, f est continue à droite de 0.
2 - Limite en e de f(x)
lim x→e x < e f(x) = lim x→e x < e x ln(x) - 1 = -∞
lim x→e x > e f(x) = lim x→e x > e x ln(x) - 1 = +∞
La courbe représentative de f admet donc une asymptote verticale d'équation x = e.
3 - Limites en +∞ de f(x)
lim
x→+∞
f(x)
x
=
lim
x→+∞
1
ln(x) - 1
= 0
La courbe Cf a une branche parabolique de direction asymptotique l'axe des ordonnées au voisinage de +∞.
4 - Dérivabilité de f à droite de 0
lim x→0 x > 0 f(x) - f(0) x - 0 = lim x→0 x > 0 1 ln(x) - 1 = 0
La fonction f est dérivable au point 0 à droite. L'équation de la tangente à la courbe Cf est :
y = 0
5 - Calcul de f '(x)
6 - Signe de f '(x) et tableau de variations
f '(x) > 0 ⇒ ln(x) - 2 > 0 ⇒ ln(x) > 2 ⇒ x > e2
Le tableau de variations est comme suit :
7 - Calcul de f "(x)
8 - Signe de f "(x) et point d'inflexion
f "(x) > 0 ⇒ -(ln(x))2 + 4 ln(x) - 3 > 0
Si on pose t = ln(x) l'inéquation devient
-t2 + 4t - 3 > 0
Nous avons ainsi une inéquation avec un polynôme de second degré qui s'annule en
t1 = 1
et
t2 = 3
Donc
f "(x) > 0 ⇒ 1 < t < 3 ⇒ e < x < e3
Le tableau de concavité de la fonction est
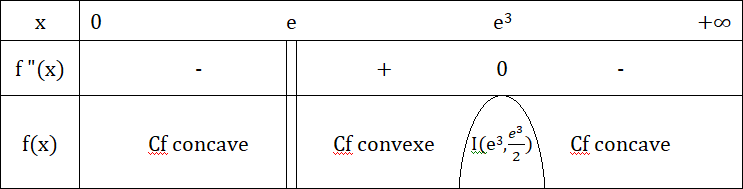
f "(x) s'annule au point e3 avec changement de signe. Le point I(e3, e3 2 ) est un point d'inflexion pour la courbe Cf.
9 - Calcul de f '(e3)
f '(e3) = ln(e3) - 2 (ln(e3) - 1)2 = 1 4
L'équation de la tangente à Cf au point d'abscisse 2
y = f '(e3) (x - e3) + f(e3) = 1 4 x + e3 4
10 - Courbe Cf